5. Прогнозування комплексного соціально-економічного розвитку країни

5.1. Загальна характеристика комплексних моделей прогнозування

Процес пізнання економічної реальності вимагає побудови економетричних моделей, причому кожна економетрична модель виходить з певної економічної закономірності, яку необхідно економічно сформулювати і кількісно визначити на основі статистичних даних.

Економетричні моделі є найбільш поширеним типом соціально-економічних моделей, які використовуються для аналізу й прогнозування комплексного розвитку країни. Вони складаються з функціональних регресійних і балансових рівнянь, які кількісно визначають взаємозв’язки і пропорції між макроекономічними величинами на всіх фазах процесу відтворення. Економетричні моделі використовувались спочатку у формі простих моделей, які описують певну частину процесу відтворення. Лише за останні десятиліття отримали розвиток складні (комплексні) економетричні моделі, покликані відображати функціонування всієї економіки. Ці моделі, поступово вдосконалюючись і пристосовуючись до потреб практики, що призводить до їх розширення і деталізації.

• Економічний зміст комплексних економетричних моделей вичерпується взаємозв’язками макроекономічних величин на окремих фазах процесу відтворення, які виражені рівняннями моделі. У зв’язку з цим економетричні моделі містять такі основні змінні й співвідношення.

• Обсяг виробленої продукції, як правило, вивчається за допомогою виробничих функцій, які виражають залежність продукції від виробничих факторів і, як зазначалося вище, головним чином від робочої сили й капіталу. Сама продукція може бути виражена як валовий випуск, валовий внутрішній продукт, національний дохід, а також валовий національний дохід. Виробничі функції звичайно дезагрегують по основних народногосподарських галузях (промисловість, будівництво, сільське господарство тощо). До специфічних факторів, що впливають на виробництво продукції, належать тренд технічного розвитку в промисловості й будівництві, індекс погоди в сільському господарстві тощо.

• Доходи та споживання населення вивчаються за допомогою функцій доходів і споживання. Доходи населення залежать від рівня зайнятості й обсягів виробленої продукції або продуктивності праці, може також враховуватися середня заробітна плата. Особисте споживання населення з точки зору попиту залежить головним чином від доходів населення і частково від рівня цін. З точки зору пропозиції — від обсягів виробленої продукції та імпорту. При цьому особисте споживання, а також відповідні індекси цін можуть дезагрегуватися за групами товарів (продовольчі та промислові, товари короткострокового і тривалого використання).

• Капіталовкладення й основні фонди вивчаються за допомогою інвестиційних функцій, а також рівнянь створення та розміщення основних фондів. Інвестиційні функції виражають залежість капіталовкладень від внутрішніх та зовнішніх факторів економічного функціонування, однак у деяких моделях, особливо короткострокових, інвестиції вважаються заданими величинами. Створення основних фондів залежить від капіталовкладень з певним часовим запізненням (лагом).
• Рівень зайнятості й безробіття моделюється за допомогою рівнянь енономічно активного та неактивного населення. З точки зору джерел ресурсів він залежить від чисельності населення працездатного віку, а з точки зору потреб — від обсягів виробленої продукції як у державі в цілому, так і в окремих галузях, від рівня і структури інвестицій, доходу. Ці змінні виявляють значну інерцію, тобто залежність від рівня зайнятості й безробіття в попередніх періодах.

• Обсяги зовнішньої торгівлі вивчаються за допомогою рівнянь експорту—імпорту. Експорт залежить від обсягів виробництва вітчизняної продукції та від обсягу імпорту з інших країн. Імпорт, з точки зору валютних ресурсів, залежить від експорту, а з точки зору потреб — від обсягів виробництва вітчизняної продукції або від споживання та інвестицій.

Макроеконометрична модель може містити також інші змінні та співвідношення процесу відтворення, які стосуються видатків, фінансів, кредиту, запасів тощо.

В економетричних моделях в основному використовуються такі визначення змінних:

• ендогенні змінні — змінні, які визначаються відповідними рівняннями моделі і є предметом дослідження;
• екзогенні змінні — змінні, які в економетричній моделі не пояснюються, а вводяться ззовні і в готовому вигляді;
• передвизначені змінні — це екзогенні й лагові (узяті із запізненням) ендогенні змінні;
• пояснюючі змінні — це передвизначені змінні та ті ендогенні змінні, які у відповідні рівняння підставляються з інших рівнянь моделі.

До екзогенних змінних належить і багато типів спеціально введених штучних змінних, що виражають вплив таких факторів, пряме статистичне вимірювання яких або неможливе, або недостатнє. До таких спеціальних екзогенних змінних головним чином відносять:

• змінні, створені на основі непрямих даних, наприклад, вплив погоди на обсяг виробництва сільськогосподарської продукції;
• лінійні й нелінійні часові тренди;
• штучні змінні, що виражають якісні або невимірювані фактори;
• інші допоміжні змінні, такі, як авторегресійні змінні тощо.

Описані взаємозв’язки і змінні можуть бути виражені за допомогою схеми (рис. 4.1.1), в якій наведені взаємозв’язки блоків ендогенних змінних, позначених прямокутниками, і блоки екзогенних змінних, позначені овалами.

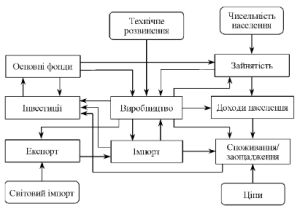
Рис. 4.1.1. Основні блоки змінних і зв’язки між ними
в комплексній економетричній моделі

Готуючи статистичні матеріали до побудови економетричних моделей, необхідно забезпечити їх порівнянність і адекватність змісту взаємозв’язків, що вивчаються. Це означає, що статистичні дані мають бути деталізовані та отримані в необхідному обсязі. Забезпечення комплексності та порівнянності даних потребує проведення різноманітних попередніх розрахунків. Найчастіше використовуються такі підходи:

• агрегація або дезагрегація даних;
• екстраполяція чи інтерполяція даних за відсутні періоди часових рядів;
• перелік вартісних показників за порівняльними цінами через індекси та коефіцієнти цін;
• розрахунок індексів, часток, середніх величин та інших похідних даних, якщо вони більше підходять для вираження деяких змінних, ніж початкові дані;
• обчислення абсолютних або відносних міжрічних розходжень;
• розрахунок запізнілих змінних (в деяких випадках зрушення на один період недостатнє, необхідно вивести зважені середні значення з більшої кількості поспіль розташованих періодів) для вираження часового зрушення в причинних зв’язках.

Через вплив на народне господарство безлічі факторів з різними причинними зв’язками і залежностями, а також різних випадкових збурень, необхідно визначити основні складові економіки і знайти найбільш суттєві змінні. В цьому розумінні рівняння, що пояснюють основні економічні явища, становлять ядро макроеконометричної моделі. Кожне таке рівняння за допомогою пояснюючих змінних виражає механізм формування певної ендогенної (залежної) змінної. В комплексних економетричних моделях в основному використовуються лінійні регресійні рівняння, які однак не обмежуються зв’язками прямої пропорційності між парами змінних, а виражають вплив множини пояснюючих факторів на залежні змінні. Коефіцієнти (параметри) регресійних рівнянь кількісно визначаються зі статистичних часових рядів (або з вибіркових даних) окремих змінних, причому враховується стохастичний характер розрахованих параметрів, і на основі тестів перевіряється їх статистична значущість. Параметри регресійного рівняння можуть бути застосовані до всіх періодів або спостережень, які обрані для їх кількісного визначення. Серед пояснюючих змінних можуть бути ендогенні, екзогенні змінні і змінні з попередніх періодів (динамічні фактори).

Тотожності (балансові рівняння) у макроекономічних моделях виражають балансові зв’язки між деякими змінними і поєднують регресійні рівняння в систему одночасних рівнянь, яка виражає також зворотні зв’язки між змінними. Ці балансові рівняння, як правило, виходять із системи національних рахунків або із системи балансів народного господарства. Часові ряди позицій цих балансів і деяких інших показників створюють базу даних для кількісного визначення параметрів комплексної економетричної моделі.

Складні макроеконометричні моделі ставлять особливо жорсткі вимоги до кількісного визначення параметрів регресійних стохастичних рівнянь, що з методологічної точки зору найбільш складно.

Використання комплексної моделі для моделювання і прогнозування може також вимагати перетворення моделі до зведеної форми з обчисленням матриць мультиплікаторів, екстраполяції екзогенних змінних і одночасного розрахунку прогнозів ендогенних змінних.

При конструюванні моделей кожне рівняння має бути кількісно визначене у варіантах, які перевіряються за допомогою методів математичної статистики. Найкращі альтернативи мають економічне тлумачення, і їх кількісне значення уточнюється через використання методів оцінки одночасних систем рівнянь. Потім перевіряється функціонування моделі в цілому.

• Побудова економетричних моделей та використання їх для прогнозування передбачає такі етапи:

1. Визначення мети дослідження. Вибір адекватної теорії, яка пояснює поведінку економічної системи. Побудова системи показників та відбір чинників, які найбільше впливають на кожний показник. Вибір форми зв’язку показників, що вивчаються, між собою і відібраними чинниками.
2. Відображення теорії у вигляді рівняння або системи рівнянь, яка пов’язує вибрані змінні. Потрібно звертати особливу увагу на випередження та запізнення впливу змінних у рівняннях, а також на змінні, які містять інформацію про перспективу. Залежно від обставин, економетричні моделі можуть включати комбінацію лінійних та нелінійних функцій. Лінійні функції привабливіші простотою, особливо це стосується стадії оцінки параметрів та прогнозування. Однак потреба розглядати такі змінні, як рівень цін та відносну швидкість зміни деякого показника (рівень інфляції), означає, що навіть прості моделі містять нелінійності.
3. Пошук відомостей про значення змінних з максимальним дотриманням теоретичних концепцій. Аналіз інформації. В ідеалі потрібні точні дані про всі необхідні змінні. Але опубліковані дані є компромісом між потребами користувачів (економістів, працівників соціальних служб, комерсантів, промисловців) та розробників (як правило, урядових статистиків). Отже, існує різниця між теоретичними поняттями та реальними даними. Окрім того, опубліковані дані до певної міри неточні через неповне охоплення, тіньову економіку, використання вибіркових оцінок замість результатів перепису, помилок в обробці даних.
4. Використання відповідних економетричних методів для оцінювання (знаходження числових значень) невідомих параметрів, які входять до рівнянь. На цьому етапі дані приводяться відповідно до теоретичної моделі й оцінюються значення параметрів. Стандартний підхід — використати один з різновидів методу найменших квадратів — реалізується за допомогою комп’ютерних пакетів. У моделях з одночасними рівняннями звичайний МНК дає зміщені оцінки параметрів через присутність ендогенних змінних у правих частинах рівнянь. Отже, потрібні інші підходи, наприклад, метод інструментальних змінних або метод систем.
5. Перевірка якості побудованої моделі, у першу чергу її адекватності досліджуваному економічному процесу. Як тільки параметри моделі оцінено, їх можна перевірити на відповідність теорії, тобто порівняти їх знаки та величини з ними. За наявності розбіжностей з теорією можна або відкинути результати, підтримуючи теорію, або відмовитись від даної версії теорії і прийняти результати. У першому випадку можна зробити висновок, що відомості ненадійні або є результатом дії аномальних факторів, і намагатись їх урахувати. В останньому випадку доцільно вдосконалити теорію, розглянувши інший набір рівнянь.
6. Знайшовши прийнятну модель, її можна використати для прогнозу. Щоб спрогнозувати значення ендогенних змінних на прогнозований період, маємо визначити величину екзогенних змінних, від яких суттєво залежить прогноз. Це можна зробити або на основі одновимірної моделі часових рядів, або використовуючи інші джерела, наприклад, іншу макроекономічну модель. Оскільки прогнозування значень екзогенних змінних вносить додаткове ускладнення, зауважимо, що його причина у використанні каузальної моделі, тобто ми здатні пояснити, якими чинниками визначається показник, а не просто переносимо поведінку в минулому на майбутнє. На основі рівнянь з оціненими параметрами і прогнозованими екзогенними змінними передбачають потрібні показники значень ендогенних змінних. Якщо потрібний прогноз на кілька періодів вперед, його можна одержати шляхом послідовності прогнозів на один період.

З аналізу соціально-економічного моделювання та прогнозування зрозуміло, що побудова обґрунтованих прогнозів вимагає не тільки коректної економічної теорії, а й правильних рішень на кожному етапі побудови прогнозу. Іншими словами, прогнози є комбінацією економічної теорії та мистецтва прогнозиста. Як наслідок, дослідження прогнозів не обов’язково може визначити, який з варіантів економічної теорії є коректним, і не завжди дає багато інформації про відмінності між економічними моделями. Може виявитись, що на точність прогнозу найбільше впливає передбачення або припущення стосовно майбутніх заходів уряду та значень екзогенних змінних.

• Макроеконометричні моделі слід будувати, починаючи з простіших моделей невеликого розміру з агрегованими даними і річним розчленуванням. Без придбання певного досвіду роботи з (невеликими за розміром) моделями неможливо приступати до побудови більш складних (ширших і детальніших) моделей. При цьому і прості агреговані моделі можуть дати гарні орієнтовні матеріали для прогнозу й імітації. Важливо, щоб модель була комплексною в розумінні вираження взаємного об’єднання всіх фаз процесу відтворення, хоча і в досить спрощеному вигляді.

Статичною моделлю, побудованою на припущенні, що народне господарство являє собою систему закритого типу без державного регулювання економіки, є спрощений варіант мультиплікаторної моделі Кейнса – ММК (див.2.1, кейнсіанська модель визначення доходу). Вона складається з двох рівнянь:

функції споживання

Сt = α + βYt + ut ; (4.2.1)

тотожності національного доходу

Yt = Ct + It , (4.2.2)

де Ct — особисте споживання в постійних цінах за період t;

Yt — національний дохід в постійних цінах за період t;

It — приватні інвестиції, плюс державні видатки, плюс баланс зовнішньої торгівлі в постійних цінах за період t. Ця змінна не пояснюється даною моделлю;

α — вільний член функції споживання виражає автономне споживання;

β — короткострокова маржинальна квота споживання. Синонімом цього виразу є короткострокова гранична схильність до споживання;

ut — збурення функції споживання.

ММК є взаємозалежною і економетричною моделлю, оскільки функція в ній містить збурення и, які вносять на економічну модель стохастичні аспекти. Іншими словами, економічна модель перетворюється на економетричну тоді, коли (в простішому випадку) в економічну модель вводяться стохастичні елементи.

Обидва рівняння ММК належать до двох, що суттєво відрізняються одна від одної, груп структурних рівнянь. Функція споживання (4.2.1) є рівнянням поведінки, а рівняння Yt — типовою балансовою тотожністю.

Рівняння поведінки, яке ще називається рівнянням реакції, описує або пояснює поведінку економічних суб’єктів (наприклад, функція споживання, функція попиту, рівняння формування цін) або наслідки цієї поведінки за певних технічних (наприклад, функція виробництва) і організаційних структур (наприклад, функція, що визначає величину податку залежно від суми доходу). Числові значення параметрів рівнянь поведінки, як правило, невідомі, їх треба визначати, оцінюючи параметри.

Тотожність відрізняється від рівняння поведінки двома особливостями: числові величини коефіцієнтів пояснюючих змінних відомі до оцінювання параметрів; у тотожності відсутні збурення.

Окреме структурне рівняння взаємозалежної системи не може бути використане для одержання повноцінного прогнозу залежної змінної. При заданих структурних коефіцієнтах α і β у функції споживання (4.2.1) необхідно знати відповідне «повної ваги» значення Yt. У разі ж прогнозування Yt через розрахункову тотожність (4.2.2) — необхідно знати (при заздалегідь відомій величині інвестицій) невідоме значення Ct. Інакше кажучи, структурні рівняння взаємозалежної системи не можуть використовуватися окремо для одержання якісного прогнозу взаємозалежних змінних.

Для прогнозування взаємозалежних змінних моделі необхідно розв’язати структурні рівняння стосовно цих змінних. В економетрії це означає перехід до прогнозованої (приведеної) форми. 

Ця форма для ММК може бути одержана простою підстановкою одного структурного рівняння в друге.

1. Прогнозована (приведена) форма функції споживання:

(4.2.3)

1. Прогнозована (приведена) форма балансового рівняння Yt :

.               (4.2.4)

У правих частинах рівнянь прогнозованої форми не зустрічається жодної взаємозалежної змінної. На діаграмі це видно з відсутності стрілок між залежними змінними (рис. 4.2.1). У рівняннях приведеної форми зустрічаються тільки екзогенні (і, можливо, лагові ендогенні) пояснюючі змінні. В ММК екзогенними є інвестиції It і допоміжна змінна xt1. Тому будь-яке рівняння приведеної форми взаємозалежної системи може використовуватися окремо для прогнозу залежної змінної.

Кожний коефіцієнт в рівняннях приведеної форми складається з різноманітних коефіцієнтів структурної форми. В ММК коефіцієнти приведеної форми є лінійними комбінаціями з α і β.

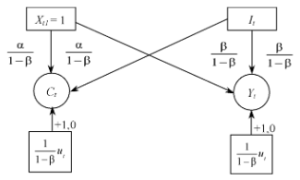
Рис. 4.2.1. Причинні зв’язки прогнозованої форми ММК

 

Структурна і приведена форми моделі доповнюють одна одну в розумінні економічної теорії. Зокрема, на прикладі моделі ММК видно, що приведена форма функції споживання Ct (4.2.3) містить екзогенну змінну It та визначає ступінь залежності між ними. Цього не можна зробити через структурну форму цієї функції (4.2.1), оскільки It не входить до неї. Тому більш-менш повну картину залежності між досліджуваними змінними для взаємозалежної моделі одержують, лише аналізуючи структурну й відповідну їй приведену форми.

Збурення в рівняннях, головна відмінність економічної моделі від економетричної, більше впливають на залежні змінні, ніж це можна припустити на основі однієї лише структурної форми. В структурній формі ММК тільки функція споживання містить збурення, а у приведеній – в обох рівняннях вони містяться у вигляді ut / (1 – β). Таким чином, структурна форма моделі не дає повної інформації про вплив збурень на залежні змінні. Це ще раз підкреслює необхідність аналізу обох форм моделі — структурної та приведеної.

Приведена форма лінійної взаємозалежної економетричної системи містить мультиплікатори. Всі мультиплікатори однакового періоду складають матрицю, відому як матричний мультиплікатор Кейнса або «мультиплікаторна матриця». Складові частини цього матричного рівняння виглядають таким чином:

;                                       (4.2.5)

,                                         (4.2.6)

де — мультиплікаторна матриця розміром 2 × 2 статичної ММК.

Взагалі, для системи лінійних рівнянь показова така обставина:

πji означає, на скільки одиниць, за інших незмінних умов, змінюється i-та ендогенна змінна уti, якщо у цей же період екзогенна змінна xtj змінюється на одну одиницю;

πji є мультиплікатором j-ї екзогенної змінної xtj стосовно і-ї ендогенної змінної уti.

Зведена форма моделі у матричному вигляді:

,                 (4.2.7)

де елементи матриць В та Г представляють собою параметри при ендогенних і передвизначених змінних в рівняннях, а елементи векторів Yt , Zt  та  ut відповідно значення ендогенних та передвизначених змінних, а також значення випадкових збурень в період t.

Вираз (4.2.7) можна записати у більш загальному вигляді:

.               (4.2.8А)

У цьому випадку параметри детермінованої частини моделі у приведеній формі –В–1Г, можна розглядати як показники, що характеризують зміну ендогенних змінних, спричинених одиничними змінами екзогенних змінних.

Для відображення в моделі державного регулювання економіки в тотожності національного доходу вводяться автономні урядові видатки (Gt):

Yt = Ct + It + Gt . (4.2.8)

Виникає одне з головних завдань економетричного моделювання і прогнозування макроекономічних систем — оцінювання впливу бюджетної і грошово-кредитної політики на зміни у поведінці змінних. В основу її розв’язку покладено також поняття мультиплікатора, яке може бути використано, наприклад, при розгляді зв’язку між змінами автономних державних витрат G і змінами національного доходу Y в моделі (4.2.1, 4.2.8).

Прогнозована форма цієї моделі для змінної Y має такий вигляд:

. (4.2.9)

Мультиплікативну реакцію доходу на зміну величини автономних витрат можна подати у формі параметра цієї змінної, тобто як величину, обернену граничній схильності до заощадження:

. (4.2.10)

Аналогічні положення стосуються будь-якої статичної лінійної стохастичної моделі, яку можна записати як (4.2.7):

BYt + ГZt = ut,

де Yt — вектор ендогенних змінних, що стосуються тільки періоду t;

Zt — сукупність екзогенно заданих змінних, які можуть включати як поточні, так і лагові значення кожної із змінних.

Подібний підхід може бути застосований і в аналізі поведінки ендогенних змінних у часі в тих випадках, коли дослідження спирається на модель, яка виражає не статичні, а динамічні закономірності, інакше кажучи, на модель, котра пояснює змін ендогенних змінних у часі. Так, будь-яка система рівнянь, яка містить лагові значення ендогенних змінних, може бути віднесена до розряду динамічних моделей, оскільки наслідки змін тих або інших екзогенних змінних будуть відчуватися за межами періоду часу, до якого вони належать. Вплив таких змін можна виявити лише при вивченні руху ендогенних змінних упродовж послідовних періодів часу (починаючи з певного моменту, коли система перебувала в рівновазі). Розглянемо, наприклад, детерміновану динамічну модель такого виду:

Ct = α + βYt–1; (4.2.12)

Yt = Ct + It + Gt . (4.2.13)

Якщо величини It і Gt залишаються у колишніх значеннях, то і значення змінної Yt при переході від одного інтервалу часу до іншого у цій моделі не змінюються. Однак, якщо G хоча б в одному періоді (t) становитиме (Gt–1 + ΔG), а потім повернеться до свого попереднього рівня, Gt–1, то розміри доходу в період (t) будуть дорівнювати (Yt–1 + ΔG), а впродовж усіх наступних періодів (t + Т) дохід становитиме (Yt–1 + βTΔG):

Yt–1 = Yt–2 ;

Yt–1 = α + βYt–2 + It–1 + Gt–1 ; (4.2.14)

Yt = α + βYt–1 + It–1 + Gt–1 + ΔG = Yt–1 + ΔG;

Yt+1 = α + βYt + It–1 + Gt–1 = α + β(Yt–1 + ΔG) + It–1 + Gt–1 = Yt–1 + βΔG;

Yt+2 = Yt–1 + β2ΔG;

…

Yt+T = Yt–1 + βTΔG, (4.2.15)

тому сумарний приріст доходу, викликаний змінами, дорівнюватиме:

.         (4.2.16)

Стосовно загальної траєкторії прямування, яку описує модель, можна стверджувати, що вона характеризується точкою стійкої рівноваги (у випадку, що розглядається — Yt–1), до якої зі збільшенням Т сходяться значення Yt+T, якщо гранична схильність до споживання (β) менша за одиницю. Так само можна показати, що, якщо величина Gt після зміни у період t, зберігає своє нове значення впродовж наступних періодів часу, дохід також поступово вийде на новий рівень, який може бути визначений зі співвідношення:

(4.2.17)

Наведений результат повністю збігається з виразом (4.2.10), оскільки за початкових умов рівноваги Yt = Yt–1 співвідношення (4.2.12, 4.2.13) стають еквівалентними (4.2.1, 4.2.8).

В економічному аналізі основний інтерес можуть викликати лише додатні значення величини β. Зазначимо однак, що, коли значення β від’ємні і за абсолютною величиною менші за одиницю, зміна Yt+T характеризується згасаючими коливаннями навкруги точки рівноваги Yt–1.

Наведена форма рівняння для змінної Yt (4.2.9), що виражається через значення, які належать до інтервалу (t – 1), повністю збігаються з виразом (4.2.14). Отже, вплив, який спричиняється зміною Gt на першому етапі, характеризується множником, що дорівнює одиниці. Аналогічний результат можна одержати із співвідношення (4.2.16), яке також описує значення кумулятивного мультиплікатора доходу для послідовних проміжків часу (якщо у ньому Т = 0).

За цією ж логікою, можна виписати різницеве рівняння першого порядку:

Yt = α + βYt–t. (4.2.18)

Розв’язати це рівняння можна за методом індукції:

Y1 = α + βY0 ;

Y2 = α + βY1 = α + (1+ β) + β2Y0;

…

.   (4.2.19)

Вираз (4.2.19) являє собою розв’язання рівняння (4.2.18), з якого одержують значення Yt у будь-який момент часу, навіть не знаючи минулих значень Yt, крім початкового, або граничного, значення Y0. Всі одержані таким чином величини YT будуть задовольняти умовам, заданим рівнянням (4.2.18). Так само можна відшукати й розв’язок системи (4.2.12, 4.2.13) щодо Yt, якщо замість величини α в (4.2.19) підставити вираз (α + It + Gt). Остаточно можна записати таке співвідношення:

Yt = βt(Y0 – Yε) + Yε, (4.2.20)

причому Yε тут визначається за умови рівноваги, Yt = Yt–1 = Yε. Коли потрібно знайти метод розв’язання системи (4.2.12, 4.2.13), значенням Yt, Yε відповідає розв’язання системи (4.2.1, 4.2.8), яка записана у зведеній формулі (4.2.9). Якщо система стійка, то при спостереженні досить тривалого періоду часу, впродовж якого Gt + It підтримується на постійному рівні, показник доходу виходить на рівноважний рівень Yt = Yt–1 = Yε і вирази (4.2.12, 4.2.13) будуть збігатися з (4.2.1, 4.2.8).

Розглянемо тепер будь-яку величину ΔG, котра доводиться до системи і викликає початкове відхилення Yt від Yε в момент t = 0:

ΔG = Y0 – Yε.

Вираз (4.2.20), так само як і розглянутий вище розв’язок (4.12.19), характеризує траєкторію повернення Yt до початкового рівня Yε, за умови, що процес не ускладнюється наступним впливом будь-яких інших зовнішніх факторів.

Така ж позиція слушна й для лінійної динамічної моделі, яка в загальному вигляді може бути записана таким чином:

BYt + ГXt +Δ1Yt–1 + … +ΔsYt–s = ut. (4.2.21)

У цій системі за пояснюючі змінні беруться як лагові значення ендогенних показників, так і поточні, або лагові екзогенні змінні. Прогнозована форма такої системи рівнянь матиме вигляд:

Yt = –B–1ГXt – B–1Δ1Yt–1 – …–B–1ΔsYt–s + B–1ut, (4.2.22)

тому граничне співвідношення між ендогенними та екзогенними змінними співпадає з аналогічним виразом, виведеним для статичної моделі (4.211):

(4.2.23)

Однак внаслідок того, що параметри зведеної форми — В–1Г стосуються тепер тільки початкового впливу зміни екзогенних змінних, їх називають мультиплікаторами початкової дії.

Якщо системі властива стійкість, то значення рівноважних або довгострокових мультиплікаторів можуть бути одержані за умови рівноваги, яка має вигляд:

Yt = Tt–1 = … = Yt–s = Yε .

У цьому випадку детермінована частина системи (4.2.22) має такий вигляд:

(B + Δ1 + … +Δs)Yε + ГXε = 0, (4.2.24)

(4.2.25)

Завдяки цьому виразу визначають ті зміни ендогенних змінних, котрі можуть викликати (коли мине досить тривалий час) постійні зміни на один відсоток кожної екзогенної змінної протягом усього періоду, що розглядається.

5.2. Складні макромоделі комплексного соціально-економічного розвитку країни

Мета цих моделей — відобразити функціонування всієї економіки. Вони поступово вдосконалюються і пристосовуються до потреб практики.

Великі економетричні моделі розвиваються головним чином у напрямі вдосконалення внутрішніх зв’язків між окремими блоками моделі й розширення її змісту, тобто у напрямі системного відображення всіх фаз процесу відтворення. Підходи до вдосконалення моделей можна розділити на дві основні групи:

• динамізація, поглиблення внутрішньої змістовності моделей;
• часова і галузева дезагрегація моделей (поява галузевих та поквартальних показників).

Перший підхід типовий для так званої голландської школи, яка заснована лауреатом Нобелевської премії професором Я. Тінбергеном. Конструкція голландських економетричних моделей має певні особливості. Більшість змінних використовується у вигляді відносних (відсоткових) річних приростів. Регресійні рівняння містять досить багато пояснюючих змінних (5—10) з різним часовим запізненням, завдяки чому досягається часткова дезагрегація і динамізація моделей.

В Голландії розробляються і використовуються також середньострокові й довгострокові економетричні моделі.

Інший підхід, типовий для так званої американської школи, характеризується галузевою і часовою дезагрегацією моделей, яка полягає у членуванні показників на галузі та квартали. Квартальні статистичні дані в більшості випадків відкориговані з урахуванням сезонів і виражені у незмінних цінах. Такі економетричні моделі є моделями середньої й великої розмірності, в результаті чого для кількісного визначення параметрів при двоступеневих оцінках доводиться використовувати деякі спеціальні методи, наприклад, метод головних компонентів.

Найбільших успіхів американська школа досягла у розробленні короткострокових моделей, для яких вихідною була модель Клєйна—Гольдбергера, опублікована 1955 р. [6]. У подальшому на її основі розробляли багато середньо- та довгострокових моделей. Модель складається з 20-ти економетричних рівнянь (в тому числі 15 регресійних стохастичних рівнянь і п’яти тотожностей). Система рівнянь містить 40 змінних (в тому числі 20 ендогенних і 20 екзогенних). Переважають рівняння лінійні. Параметри моделі розраховані на основі річних статистичних даних національних рахунків США за 20 років.

Типовим прикладом екстенсивного підходу до побудови комплексної економетричної моделі є «Брукінгська модель» [6], яка з’явилася в 1965 р. і започаткувала перехід від окремих економетричних моделей до комплексних. Вона належить до найбільш широких короткострокових економетричних моделей. Її підмоделі у початковому варіанті містили 359 рівнянь, кількість яких при включенні їх у комплексну модель була зменшена до 170 регресійних і 56 балансових. У розрахунках параметрів моделі було використано декілька методів, причому модель необхідно було привести до блочно-рекурсивної форми, оскільки часові ряди за 60 кварталів були недостатніми для одночасного кількісного визначення всіх рівнянь. Модель продовжує вдосконалюватися і використовується для імітації альтернатив економічної політики.

Економетричні моделі в країнах Східної Європи почали застосовуватися на початку сімдесятих років. Найбільш суттєвих результатів у побудові комплексних економетричних моделей народного господарства досягнуто в Росії, Україні, Угорщині, Польщі.

Серед перших макроекономічних моделей України були економетричні моделі УКР-1 та УКР-2, розроблені в НДУ при Держплані УРСР. Модель УКР-1 визначала основні агреговані республіканські показники за допомогою 13 стохастичних регресійних рівнянь і 2 тотожностей, які утворюють динамічну одночасну систему. Повторюючи загальну тенденцію розвитку економетричних моделей, на подальшому етапі досліджень модель УКР-1 оформилася в дезагреговану за галузями модель УКР-2. Ця модель була детальнішою і пристосованішою до існуючої на той час планової методики. Її структуру формували 7 взаємопов’язаних блоків («Промисловість», «Сільське і лісове господарство», «Будівництво», «Транспорт і зв’язок», «Торгівля і громадське харчування», «Інші галузі матеріального виробництва», «Підсумкові республіканські показники»). Модель УКР-2 вважалась дезагрегованою моделлю великого розміру. Вона мала 79 регресійних та 22 балансових рівнянь.

Сучасні економетричні моделі характеризуються більш детальним розробленням комплексних моделей. Оскільки практичне застосування моделей пов’язане з різними труднощами, їх розвиток спрямовується на побудову систем моделей, які ефективніше відображають різні аспекти розвитку економіки. Системи моделей створюються на рівні окремих країн (французька, італійська, німецька), на рівні господарств кількох країн (західноєвропейських, східноєвропейських, Америки і Канади та ряду інших) і на рівні світового господарства в цілому.

• Інститутом економіки НАН України і Міжнародним центром інформаційних технологій та систем НАН та Міносвіти України розроблено кілька версій систем макроеконометричних моделей прогнозування економіки України УКР-МАКРО. Метою побудови взаємопов’язаної системи макроеконометричних моделей, за допомогою якої можливе прийняття вірогідних рішень, є характеристика розвитку економіки України в перехідний період на макрорівні за різними сценаріями.

Перші дві версії — УКР-МАКРО1 і УКР-МАКРО2 побудовані на основі макропоказників за схемою балансу народного господарства. З 1995 р. розроблена нова версія моделей прогнозування — УКР-МАКРО3 за системою національних рахунків.

На рис. 4.3.1 подана структурна схема взаємозв’язків підсистем у скороченій системі моделей економіки України.

Зовнішнє середовище визначено формуванням населення, зовнішньо-економічною діяльністю, інфляційними процесами. Основними підсистемами у системі УКР-МАКРО3 є:

• виробництво;
• зайнятість та безробіття;
• фонди та капітальні вкладення.

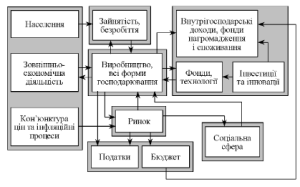
Рис. 4.3.1. Взаємозв’язки блоків-підсистем комплексу
моделей прогнозування соціально-економічного розвитку України

 

Розширена модель включає також підсистеми:

• фінанси та податки;
• соціальна сфера;
• ринок товарів та послуг.

В умовах перехідної економіки виникає ряд труднощів, до яких відносять:

• прогнозування вартісних макроекономічних показників за умов інфляції;
• врахування темпів виробничого спаду в трансформаційний період;
• врахування залежності економіки від імпорту енергоносіїв, новітніх технологій, продовольства і товарів широкого вжитку.

Для прогнозування вартісних макроекономічних показників за умов інфляції пропонується така схема:

1. Вирізняється один чи декілька основних базових показників, динаміка яких прогнозується, абстрагуючись від інфляції, у порівняних цінах.
2. Вводяться показники інфляції через співвідношення базових показників у фактично діючих цінах до їх значення у порівняних цінах.
3. Прогнозуються інші вартісні показники у фактично діючих цінах з урахуванням показника інфляції.

У цьому дослідженні базовим показником обрано обсяг валового внутрішнього продукту (ВВП) у постійних карбованцях 1990 р. Введено дефлятор ВВП, розрахований як відношення номінального ВВП у фактично діючих цінах до його значення у порівняних цінах 1990 р. Дефлятор валового внутрішнього продукту використовувався у системі як показник, що відображає інфляційні процеси. Він же як будучи екзогенна змінна визначався через експертизу на етапі розв’язання системи моделей в імітаційному режимі. Прогнозування інших вартісних оцінок здійснено у фактично діючих цінах з урахуванням інфляції через дефлятор ВВП.

У системі УКР-МАКРО3 моделювання змін ВВП здійснюється відповідно до виробництва головних для країни продуктів та їх реального товарообігу в натуральному обчисленні. Продукти, розглянуті в системі моделей, представляють різні галузі промисловості і сільського господарства, тобто видобуток, виробництво сировини і матеріалів, продуктів кінцевого споживання та електроенергії, товарів народного споживання, головних продуктів сільського господарства та харчової промисловості, а також показники вантажообігу транспорту та введення в експлуатацію житла.

На рис. 4.3.2 подана схема причинно-наслідкових зв’язків між показниками, що входять до системи УКР-МАКРО3.

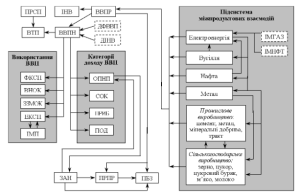
Рис. 4.3.2. Підсистеми «Макропоказники» і «Міжпродуктові взаємодії» в УКР-МАКРО3

 

На рис. 4.3.2 екзогенними змінними є:

• ДФВВП — дефлятор ВВП;
• ІМГАЗ — імпорт газу;
• ІМНФТ — імпорт нафти.

Ендогенні змінні:

ВВПР — реальний ВВП у порівняних цінах 1990 р.;

ВВПН — номінальний ВВП у фактично діючих цінах;

ПРСП — проміжне споживання;

ВТП — випуск товарів та послуг;

ЗАН — кількість зайнятих;

ПРПР — продуктивність праці;

ПБЗ — приховане безробіття.

Показники за категоріями використання номінального ВВП:

ФКСП — фактичне кінцеве споживання;

ВНОК — валове нагромадження основного капіталу;

ЗЗМОК — зміна запасів матеріальних обігових коштів;

ЕКСП — експорт товарів та послуг;

ІМП — імпорт товарів та послуг.

Показники формування номінального ВВП за категоріями доходу:

ОПНП — оплата праці найманих працівників;

СОК — споживання основного капіталу;

ПРИБ — прибуток;

ПОД — податки на виробництво та імпорт, за винятком субсидій.

Згідно зі схемою модель економічного розвитку в цій системі складається з двох частин:

• виробництво основних продуктів у натуральному обчисленні;
• вартісні макропоказники за системою національних рахунків.

Перша частина системи моделі міжпродуктових взаємодій складається з 28 співвідношень, з яких 24 є стохастичними регресійними рівняннями, а 4 — трендами. Цю модель можна характеризувати як модель міжпродуктових взаємодій, оскільки обсяги виробництва одних видів продукції моделюються в ній залежно від обсягів виробництва інших (сировини, матеріалів, палива або устаткування), необхідних для процесу виробництва тих видів продукції, що моделюються.

Крім елементів першої частини моделі, до пояснюваних змінних відносять також елементи зовнішнього середовища, які відображають обсяги ввезення енергоносіїв, зокрема нафти та газу. Безумовно, треба враховувати сукупний експорт-імпорт усіх, без винятку, товарів. Проте це не завжди вдається, оскільки зведена інформація з цього приводу, на жаль, недостатньо вірогідна, а інколи і зовсім відсутня.

Зростання обсягів виробництва основних видів продукції в моделі представлено динамічним варіантом виробничої функції, яка ґрунтується на припущенні взаємодоповнюваності виробничих чинників.

Підсистема міжпродуктових взаємодій пов’язана з вартісними макропоказниками через реальний ВВП. Щоб врахувати спад виробництва за умов інфляції, реальний ВВП моделювався у постійних карбованцях 1990 року від обсягів виробництва основних видів продукції у натуральному виразі. Для цього в модель були введені часткові прогнози реального ВВП, які визначалися залежно від рівнів виробництва кожного з видів продукції.

На основі часткових прогнозів реального ВВП був розрахований реальний ВВП як їхнє середнє арифметичне.

Номінальний ВВП у фактично діючих цінах визначається в моделі як добуток реального ВВП і показника інфляції — дефлятора ВВП.

У систему рівнянь міжпродуктових взаємодій, що описують виробництво електроенергії, вантажообіг транспорту, виробництво сільськогосподарської продукції, входять показники: імпорт нафти та імпорт газу, які є важливим джерелом енергоресурсів для України і саме тому обрані керуючими у версії УКР-МАКРО3.

Через штучні змінні, які вводяться до рівнянь виробництва сільськогосподарської продукції, відображається вплив випадкових чинників, зокрема погодних умов (у сценарних розрахунках: були вони сприятливі чи несприятливі). До рівняння, що описує виробництво вугілля, була введена і така змінна, що відбиває його спад внаслідок соціальної напруги серед шахтарів. Використання цієї змінної дало змогу в прогнозуючих оцінках урахувати стабільну чи нестабільну ситуацію у вугільній промисловості.

Таким чином, у версії УКР-МАКРО3 реальний ВВП моделюється залежно від виробництва головних продуктів у натуральному виразі, а також від імпорту енергоносіїв, погодних умов та соціальних ситуацій, особливо у вугільній промисловості.

У другій частині системи моделей УКР-МАКРО3, яка збігається з новою версією УКР-МАКРО4, представлені макропоказники відповідно до системи національних рахунків.

У цій версії системи моделей зроблено спробу моделювання економічного розвитку залежно від стану інвестування.

Між обсягами інвестицій та економічним зростанням існує тісний зв’язок. Отже, основним завданням моделі є оцінка цього впливу на альтернативні прогнозовані рішення щодо зміни економічного стану залежно від розміру частини інвестицій у реальному ВВП, яка прийнята в системі екзогенною — керуючою змінною. Тобто на етапі одержання прогнозуючих оцінок частка інвестицій у реальному ВВП на майбутнє має задаватися експертним шляхом.

Рівняння для вартісних макропоказників як для системи УКР-МАКРО3, так і для системи УКР-МАКРО4 мають однаковий вигляд і їх моделювання здійснюється в реальному вимірі, тобто з урахуванням інфляції через коригування цих показників на дефлятор ВВП. Згідно з системою національних рахунків у моделі розрізняються показники, які формують ВВП за категоріями доходу, і показники за категоріями використання ВВП.

На етапі прогнозування за системою УКР-МАКРО3 було розглянуто два варіанти сценаріїв — оптимістичний і песимістичний. В системі УКР-МАКРО3 керуючими змінними є обсяги імпорту нафти та газу, рівні інфляції. У системі також є такі фонові змінні, як погодні умови та ситуація у вугільній промисловості. Оптимістичний погляд полягає в тому, що постачання енергоносіїв буде здійснюватись наростаючими темпами як для нафти, так і для газу; погодні умови — сприятливі, ситуація у вугільній промисловості — стабільна. Песимістичний прогноз передбачає продовження спаду у постачанні енергоносіїв, але темпи падіння дещо уповільнюються; погодні умови — несприятливі, ситуація у вугільній промисловості — нестабільна.

За системою УКР-МАКРО4 було також розглянуто два варіанти прогнозованих рішень: уповільнене чи прискорене зростання частки інвестицій у реальному ВВП.

• Інститутом економічного прогнозування НАН України розроблена «Макромодель економіки України — 1». Модель зорієнтована на складання середньострокових прогнозів розвитку ключових макроекономічних показників [20]. Модельні зв’язки розглядаються у секторному розрізі на основі показників і залежностей Системи національних рахунків (СНР) України з врахуванням цілей економічної політики.

Зазначена економетрична модель має блочну структуру і призначена для обрахування прогнозних показників у щорічному вимірі. Взаємодія одночасових блоків виявляється у побудові та узгодженні ключових індикаторів платіжного та монетарного балансів, СНР та балансу державного бюджету.

Ендогенними змінними цієї економетричної моделі є такі: обсяг ВВП, обсяги приватного, державного та загального споживання, величина основних фондів та валових інвестицій, зміна запасів оборотних коштів, обсяги імпорту та експорту (подаються у фактичних та базисних цінах), рівень зайнятості, сальдо державного бюджету, обсяг загальних державних витрат, характеристики загального доходу та загальної пропозиції.

Екзогенними модельними змінними виступають: обсяг світового ВВП; дефлятори вітчизняного та світового ВВП, приватного та державного споживання, валових інвестицій, зміни запасів матеріальних оборотних коштів, експорту та імпорту; індекси споживчих цін та цін промислового виробництва; кредитна відсоткова ставка; частка бюджетних надходжень та витрат у ВВП.

Змінними економічної політики визначаються: реальне та державне споживання, валові інвестиції, ставки окремих податків, експорт, імпорт, а також процентні ставки, валютний курс та індекс інфляції.

Взаємодія блоків моделі реально виявляється у побудові та узгодженні основних показників платіжного і монетарного балансів, системи національних рахунків (СНР) та балансу державного бюджету. До того ж виробництво, дохід і витрати (або заощадження) як відомо, мають три основні взаємозалежності: виробництво — дохід; дохід — витрати; заощадження — придбання активів.

Поточні й капітальні взаємозв’язки СНР між державним, приватним, зовнішнім секторами та монетарною системою як посередницьким сектором і три вищенаведені базові взаємозалежності складають тотожності національного доходу. Вони відображають обмеження бюджетного, зовнішнього і грошово-кредитного секторів і використовуються для розроблення системи секторальних макромоделей оцінки і прогнозування економіки України (рис. 4.3.4.).

У макромоделі трансформація та дезагрегація балансових макроекономічних взаємозв’язків і тотожностей національного доходу ґрунтується на вищенаведених методах регресійного аналізу (розд. 2) і методології конструювання систем відповідних економетричних моделей.

• Модель реального сектора містить базові макроекономічні тотожності, на основі яких формуються складові ВВП за різними методами обрахування. У моделі виділено два блоки. Блок пропозиції формує виробничу функцію (сума валового внутрішнього продукту та імпорту), що залежить від основних фондів, зайнятості та імпорту кінцевих товарів і послуг і лагових змінних. У блоці наявні функції зайнятості та основних фондів.

Агрегований попит визначається як використання валового внутрішнього продукту і формує обсяги кінцевих споживчих витрат домашніх господарств, сектора загального державного управління, валового нагромадження основного капіталу, зміни запасів матеріальних оборотних коштів та експорту товарів і послуг.

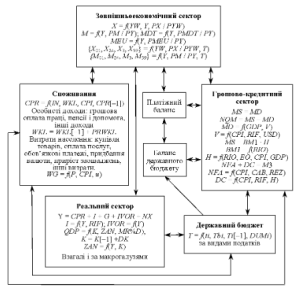
Рис. 4.3.4. Секторальні макромоделі економічного прогнозування

 

Пояснення до рис. 4.3.3.:

Y, GDP — валовий внутрішній продукт (ВВП);

CPR — споживання домашніх господарств (приватне);

І — валові інвестиції;

QDP — загальна пропозиція;

К — основний капітал (основні фонди;

DК — приріст основного капіталу;

ZAN — зайнятість;

P — виробництво ВВП на одного зайнятого (або продуктивність праці);

WG — середньомісячна заробітна плата зайнятого у народному господарстві;

u — рівень безробіття;

NX — чистий експорт товарів і послуг;

Х — експорт товарів і послуг;

М — імпорт товарів і послуг;

MDT — імпорт послуг;

MEU — імпорт машин та устаткування;

Х01 — експорт продовольчих товарів;

Х24 — експорт сировини;

Хз — експорт проміжної продукції;

X59 — експорт готової продукції;

М01 — імпорт продовольчих товарів;

М24 — імпорт сировини;

Мз — імпорт проміжної продукції;

M59 — імпорт готової продукції;

MD — попит на гроші;

MS — пропозиція грошей в економіку;

MD — попит на гроші;

RW — процентна ставка;

PMEU, PMDT, PY, РХ, РМ — відповідні індекси цін;

PYW — індекс цін (дефлятор) світового ВВП;

IVOR — змінна запасів обігових коштів, у цінах поточного періоду;

IWKL(–1) — сума заощаджень на початок року;

WKL — сума заощаджень на кінець року;

ІN — особисті доходи домашніх господарств після сплати податків;

YW — світовий ВВП;

MS — пропозиція грошей в економіку;

ВМ1 — грошовий мультиплікатор;

Н — грошова база;

NQM — показник дисбалансу або нерівноваги грошового ринку;

MSF, MDF — прогнозовані значення попиту та пропозиції грошей (відповідно);

RIO — ставка рефінансування НБУ (офіційна);

ЕО — офіційний обмінний курс національної грошової одиниці;

USD — рівень доларизації;

MQ — грошова маса (квазі-гроші);

NFA — чисті зовнішні активи;

М1 — грошова маса (агрегат М1);

М3 — грошова маса (агрегат М3);

REZ — зміни валютних резервів країни;

СРІ — індекс споживчих цін;

CAB — сальдо поточного рахунку (платіжний баланс);

DC — внутрішній кредит;

RIF — ставка рефінансування НБУ (фактична);

Ti — сума податку і-го виду;

tі — ставка податку і-го виду;

Tbi — податкова база і-го виду;

DUMi — фіктивна змінна, яка визначає організацію збору і дискреційний ефект податку і-го виду.

Обидва виділені в моделі блоки тісно пов’язані зі змінними кредитно-грошового, зовнішньоекономічного секторів, фінансів і споживання. Рівняння та тотожності моделі охоплюють основні макрогалузі і господарчі комплекси національної економіки: промисловість у розрізі паливно-енергетичного, металургійного, хімічного комплексів, комплексу будівельних матеріалів, легкої та харчової промисловості; сільське і лісове господарство; будівництво; транспорт та зв’язок; сферу обігу та інші макрогалузі.

• Модель сектора споживання та доходів населення визначає функцію споживання, основні види доходів та витрат населення. Приватне споживання (кінцеве споживання домашніх господарств) пояснюється динамікою його лагового значення, особистих доходів домашніх господарств, суми заощаджень та індексу інфляції. Розглядаються модельні оцінки адресних субсидій населенню (на оплату житла), особистих грошових доходів домашніх господарств до і після сплати податків, особисте споживання, платоспроможний попит, грошова оплата праці (в цілому), середньомісячна заробітна плата зайнятих у народному господарстві, оплата послуг населення, купівля товарів, обов’язкові платежі та інші доходи і витрати населення.

• Модель державного сектора наводить функцію державного споживання (споживання сектора державного управління), основні види бюджетних надходжень та видатків, їхні загальні суми та баланс бюджету. Прогнозування надходжень ґрунтується на наявності зворотних зв’язків між податковими ставками і податковими базами, взаємозалежності всіх секторів економіки і обрахуванні доходів на основі функцій, які будуються для різних видів податків, виходячи з прогнозуючих оцінок відповідних баз оподаткування. Тобто загальний вигляд суми окремих надходжень формується у моделі як функція від відповідної ставки податку, податкової бази та змінних, що характеризують ефективність роботи податкової адміністрації. Відповідно до структури бюджету України пропонується модельне визначення таких основних видів бюджетних надходжень: податку на прибуток підприємств і організацій, податку на додану вартість (ПДВ), акцизного збору, прибуткового податку з громадян, плати за землю, державного мита, надходження коштів від приватизації державного майна та інші. Вибір цих складових ґрунтується на тому, що вони визначають найбільш вагомі частки бюджетних надходжень і охоплюють їх більш ніж на 80 %.

При прогнозуванні надходжень слід ураховувати наявність зворотних зв’язків між податковими ставками і податковими базами, що можливо при використанні макроекономічної моделі, яка визначає взаємозв’язки між усіма секторами економіки. Крім того, загальна економетрична модель на макрорівні надає можливість обрахування доходів на основі функцій, які будуються для різних видів податків, виходячи з прогнозуючих оцінок відповідних баз оподаткування.

Після визначення класифікації доходів бюджету для підготовки прогнозів використовується податкова функція, через яку розраховують надходження від того чи іншого податку залежно від величини приблизної податкової бази.

• У моделі зовнішньоекономічного сектора визначаються макрозмінні експорту, імпорту та їхніх складових відповідно до стандартів міжнародної класифікації: експорт та імпорт продовольства, сировини та матеріалів, проміжної та кінцевої продукції. Функція загального експорту залежить від динаміки вітчизняного і світового ВВП та паритету дефляторів ВВП і експорту. Загальний імпорт та його агрегатні складові: імпорт послуг, імпорт машин і обладнання та інший імпорт моделюються під впливом динаміки реального ВВП і співвідношення відповідних дефляторів ВВП та визначених у моделі категорій імпорту.

• Модель грошово-кредитного сектора ґрунтується на припущенні рівності попиту і пропозиції грошей. Вихідними змінними є прогноз грошових агрегатів, грошової бази НБУ залежно від поставленої мети щодо зростання ВВП, рівня інфляції та значення обмінного курсу гривні. В моделі проводяться також прогнозні розрахунки показників грошового ринку, за допомогою яких можна не тільки аналізувати поточну ситуацію та оцінювати можливість застосування тих чи інших інструментів монетарної політики, а й відзначити фактори, динаміка яких може вплинути на виконання цільового орієнтиру економічного зростання: грошового мультиплікатора, швидкості обігу грошей, внутрішнього кредиту, зовнішніх активів.

В Інституті економічного прогнозування НАН України здійснена часткова реалізація наведених секторальних моделей. Модель розроблено на основі існуючих у світовій практиці з метою отримання середньострокових оцінок розвитку національної економіки і пошуку можливостей регулювання її розвитку за допомогою набору управляючих змінних за умов економічної рівноваги. Складається вона з 33 стохастичних регресійних рівнянь та тотожностей і належить до нелінійної, агрегованої моделі, яка містить одночасові блоки. Генерація стохастичних регресійних рівнянь здійснювалась на основі часових рядів методами найменших квадратів і автокореляції залишків першого порядку. Для моделювання регресійних рівнянь використовувались лінійні, гіперболічні та логарифмічні функції, а також лагові й фіктивні змінні, за допомогою яких згладжувались стрімкі зміни тенденцій динаміки змінних (розд. 2).

На базі цієї моделі була розрахована більшість макропоказників середньострокового прогнозу економіки України. Наведено можливі найбільш низькі, ймовірні та верхні межі коливання реального виробництва (ВВП) та індексу інфляції, а також сценарії (ймовірний, оптимістичний, песимістичний) можливих змін основних агрегатів розподілу ВВП, бюджетних і грошово-кредитних показників.

• Певний інтерес представляє розробка Інституту кібернетики ім. В.М. Глушкова НАН України — моделююча система “Бюджет”, яка призначена для вирішення задач бюджетного та макроекономічного моделювання, зокрема, оцінки очікуваних надходжень в держбюджет і обсягів його найважливіших витрат, прогнозування динаміки цін, обсягів платоспроможного попиту, експортно-імпортних потоків тощо. Дана система побудована за блочним принципом, кожен із 8 блоків є окремою економіко-математичною моделлю або групою моделей.

Основу блоку “Виробництво” складають рівняння міжгалузевого балансу в базових цінах. У цьому ж блоці за нормативами балансу та галузевими індексами діючих цін, що розраховані відносно базових, визначаються величини відносної собівартості продукції кожної із галузей.

У блоці “Фінанси виробників та споживачів” розраховуються номінальні доходи та витрати виробників (з їх галузевою диференціацією) і споживачів. Модель дозволяє розрізняти групи споживачів за такими ознаками, як джерело отримання та величина доходів, соціальний статус тощо. Загальне (суспільне) споживання та його окремі складові, що фінансуються з державного бюджету, також можуть розглядатися у розрізі споживачів.

Платоспроможний попит споживачів залежно від їх прибутків, грошових накопичень і діючих цін, а також сукупний попит на інвестиції з боку виробників та держави визначається у блоці “Попит”.

У блоці “Бюджет” здійснюється розрахунок головних нормативів консолідованого бюджету та визначається їх вплив на собівартість продукції та обсяги виробництва (через податкові ставки, з одного боку, і прямі та опосередковані субсидії, державні інвестиції — з другого), на попит споживачів (через заплановані витрати на суспільне споживання) і на інші фінансові показники. Реалізовано декілька стратегій субсидування виробництва, зокрема, фіксації деяких цін на заданому рівні з покриттям частини витрат виробників з держбюджету. Модель визначення обсягів субсидування, необхідних для забезпечення цієї стратегії, також входить в даний блок .

Розрахунок діючих цін здійснюється в блоці “Ціни”, причому сюди входять моделі витратного, монопольного, олігопольного, конкурентного та інших механізмів ціноутворення.

У блоках “Експорт” та “Імпорт” здійснюється прогнозний розрахунок обсягів цих показників.

Блок “Макроекономічні показники” призначений для розрахунку змін грошової маси в обігу, курсів обміну національної валюти, агре-гованих показників цін (дефлятор ВВП, індекс споживчих цін) та інших макроагрегатів.

Моделююча система “Бюджет” використовувалася для аналізу проекту бюджету на 1996 р. в контексті сценарного моделювання: було розглянуто оптимістичний, реалістичний та помірно песимістичний сценарії. За кожним з них припускається, що монетарні показники є основними впливовими чинниками економічної стабілізації, а варіація їх величин залежить від певних (для кожного сценарію — своїх) параметрів грошово-кредитної політики. На основі кожного виду сценарію надаються прогнози динаміки цін та оцінки гранично можливих обсягів грошової маси в обігу.

• Інша модель середньострокового прогнозування розроблена в Інституті кібернетики ім. В.М. Глушкова НАН України (автори-розробники — Б.Панасюк, І. Сергієнко, Л. Гуляницький). Дана економетрична модель призначена для розрахунку щорічних темпів росту ключових макроекономічних змінних (реального ВВП, рівня інфляції та безробіття) і базується на використанні виробничих функцій типу Кобба-Дугласа.

Екзогенні змінні моделі (які віднесені авторами до чинників економічного зростання, що формують пропозицію) характеризують наявність працездатного населення, рівень безробіття, індекс матеріальних витрат, величину виробничого основного капіталу, завантаженість основного капіталу (виробничих потужностей), зношеність основного капіталу, обсяг капітальних вкладень, паливно-енергетичний баланс. Кількісна оцінка ВВП з боку сукупного попиту конкретизується за допомогою показників оплати праці, чисельності працездатного населення, фонду споживання, фонду накопичення, рівня інфляції.

Дана модельна розробка фактично передбачає використання двох моделей — степеневої квартальної моделі та лінійної річної (залежно від формалізації виробничої функції, що описує динаміку реального ВВП).

Степенева модель складається з 8 стохастичних рівнянь, на основі яких здійснюються прогнозні розрахунки реального ВВП, задіяних обсягів основного виробничого капіталу, частки задіяних трудових ресурсів, обсягів капітальних вкладень та обсягів прибутку підприємств. При цьому враховуються такі керуючі параметри, як частка безробітних, ступінь зносу та використання основного виробничого капіталу, коефіцієнти матеріаломісткості, базисні та поточні податкові ставки (ПДВ та податку на прибуток). Лагові змінні інвестиційних вкладень охоплюють період до двох років. Для переходу від реального до номінального виміру ВВП в моделі розраховується агрегований показник цін (дефлятор ВВП).

Особливістю зазначеної моделі є використання експертних оцінок для коригування статистичних даних, що характеризують період початку 90-х років. Також експертним шляхом визначаються межі, в яких знаходиться траєкторія динаміки ВВП, а потім знаходяться модельні параметри, за яких прогнозна крива значень ВВП вкладається в зазначені межі.

Лінійна модель призначена для складання довгострокових прогнозів і у робочому варіанті містить три основні функціональні залежності для визначення реального обсягу ВВП: визначається величина задіяного капіталу як функція від величини (бажаного) основного капіталу, обчисленої на кінець періоду за балансовою вартістю та ступеня його спрацювання; визначається частка задіяних трудових ресурсів, що залежить від чисельності працездатного населення та ступеня використання основного капіталу; величина реального ВВП в цінах 1992р. є адитивною функцією, що містить дві вищезазначені залежності та характеристику впливу стохастичних змінних. На базі лінійної моделі вирішується задача квадратичної оптимізації з неточно заданими даними, причому траєкторія динаміки ВВП визначається експертним шляхом; для вирішення задачі авторами розроблений та комп’ютерне реалізований програмний комплекс. Це дає змогу здійснювати прогнозні розрахунки за двома сценарними варіантами розвитку економіки України — помірним та мінімальним.

Серед менш масштабних моделей слід виділити дві макроеконометричні розробки (мономоделі), які є перспективними в аналітичному плані використання. 

• Квартальна (річна) модель прогнозного розрахунку реального ВВП, що базується на використанні методу групового врахування аргументів (МГВА), розроблена в Кібернетичному Центрі НАН України під керівництвом О.Г. Івахненка.

Технологічною основою цієї моделі є метод групового врахування аргументів. Це — індуктивний переборний метод, який має переваги для складно-структурованих систем, зокрема для об’єктів з розмитими характеристиками (неповною вихідною інформацією). Алгоритми МГВА знаходять єдину оптимальну для кожної вибірки модель за допомогою певного перебору всіх можливих моделей-кандидатів та операції їх оцінки за зовнішнім точнісним чи балансовим критерієм на незалежній вибірці даних. Вихідною моделлю є краща з множини моделей-кандидатів — та, що веде до мінімального значення зовнішнього критерію.

Модель, що базується на використанні МГВА, придатна для прогнозних розрахунків реального обсягу ВВП, рівня реальних доходів населення та інших макропоказників. Для їх обрахунку використовувались квартальні та річні значення 82 макроекономічних та демографічних показників починаючи з 1992 p., які могли впливати на досліджувані фактори. Згідно з результатами застосування модельного підходу, найбільш впливовими виявилися показники обсягу реального ВВП, зростання грошової бази, аукціонного обмінного курсу, дефлятора ВВП, індексу оптових цін, обсягу валової сільськогосподарської продукції, рівня середньої продуктивності праці, чисельності безробітних та їх частки від загальної робочої сили, обсягу грошових доходів населення, величини кредиторської заборгованості підприємств, обсягу імпортопостачання.

Прогнозна модель з використанням МГВА формально є лінійною багатрфакторною регресією і може використовуватися для середньо-та довгострокового прогнозування.

• Довгострокова економетрична модель економічного зростання у перехідних економіках була розроблена співробітниками МВФ О. Гав-рилишиним, І. Ізворскі, Р. Рооденом. У даній розробці автори використали регресійний аналіз, виділяючи кілька впливових факторів, що характеризують інституційні зміни в економічному середовищі.

Ендогенною змінною моделі є темп зростання реального ВВП.

Екзогенними змінними виступають такі показники: темп інфляції (характеризує макроекономічну політику), індекс структурної реформи (опосередковує рівень реалізованих структурних реформ), обсяг урядової діяльності, який вимірюється державними витратами як відсотком від ВВП (демонструє прояв економічних спотворень, зумовлених високим рівнем оподаткування та бюрократизації).

У цій моделі присутні змінні, які характеризують два види “стартових умов”, одна з них охоплює макроекономічні спотворення та незнання ринкових процесів, а друга — рівень розвитку соціалістичної економіки та асоційованих з ним спотворень.

Модель було проаналізовано за допомогою групових даних для 25 країн з перехідною економікою за 1990-1997 pp. (200 спостережень). Особливістю даної моделі є варіантність та специфіка її використання. У першому випадку автори здійснювали декомпозицію ретроспективного періоду на періоди 1990-1993 pp. та 1994-1997 роки. У другому випадку застосовували деталізацію індексу структурних реформ, що передбачає введення додаткових незалежних змінних: субіндексу структурних реформ для лібералізації внутрішніх цін, субіндексу структурних реформ для приватного входу на ринок, субіндексу структурних реформ для лібералізації торгівлі та системи обмінного курсу, субіндексу структурних реформ для правової реформи.

Модель формалізована у вигляді лог-лінійної багатофакторної регресійної залежності.