4.1. Методи фільтрації сезонної компоненти. Часові ряди з інтервалом менше року (місяць, квартал) як правило, містять сезонність. Сезонна компонента має період m: (m = 12 для ряду місячних даних; m=4 – для ряду квартальних даних). Окрім того, відомо, що m кратне n, тобто , k – ціле число. Очевидно, якщо m – кількість місяців або кварталів в році, то k – кількість років, представлених у часовому ряду {уt}. Тому вхідні дані тренд-сезонного часового ряду часто представляються у вигляді матриці {} розміру [kхm]. У цьому випадку тренд-сезонна модель (1.2.2) записується із врахуванням подвійної індексації:
, ; j = . (4.1.1)
Співвідношення, що встановлюють зв’язок між індексами t та (i,j) мають вид:
; [] означає цілу частину числа. (4.1.2)
Існує декілька методик оцінки сезонної компоненти. Основні відмінності їх полягають у тому, в якій послідовності та якими методами виділяти складові часового ряду, на якому етапі вважати точність виділених складових задовільною.
Перш за все перевіряється гіпотеза про наявність або відсутність сезонних коливань, оскільки часовий ряд не завжди містить сезонну складову. Для оцінки впливу сезонності на досліджуваний показник іноді достатньо економічного (змістовного) аналізу і графічного відображення спостережень за два-три роки. Коли ж ступінь коливань не дуже велика, можна використати спеціальні статистичні критерії: дисперсійний, автокореляційний, гармонічний тощо. Їх суть зводиться до перевірки на випадковість залишкової компоненти ряду, з якого вилучений тренд.
При підтвердженні існування сезонного процесу здійснюється фільтрація сезонної компоненти. Більшість методів фільтрації побудовано таким чином, що попередньо виділяється тренд. Визначити наявність у часовому ряду тренду і встановити ступінь його гладкості можна за допомогою статистичних методів, розглянутих у розділі 1.3. Після виділення тренду залишаються сезонна компонента разом із випадковою . Розділення сезонної та випадкової компонент починається завжди з виділення сезонної компоненти і якщо усі складові знайдені правильно, то залишки мають властивості “білого шуму”.
При дослідженні сезонної хвилі частіш за все припускається, що вона не змінюється з року в рік, тобто: , i+m≤ k. Насправді таке припущення далеке від дійсності, принаймні для більшості економічних процесів. Для сезонної хвилі характерна зміна з часом як її розмаху, так і форми. В результаті виникає необхідність в аналізі і передбаченні змін сезонної хвилі.
Фільтрація сезонної компоненти за допомогою індексу сезонності. Найпростішим способом, який характеризує коливання рівнів досліджуваного показника, є розрахунок питомої ваги кожного рівня у загальному річному обсязі або індексу сезонності.
Розглянемо наступну модель:
, (4.1.3)
де – «річна» складова (тренд);
– індекс сезонності або стала пропорційності для j-го кварталу (місяця), яка є безрозмірною величиною і не змінюється з року в рік.
Індекс сезонності 1j характеризує ступінь відхилення рівня сезонного часового ряду від ряду середніх (тренду) або, кажучи інакше, ступінь коливань відносно 100%. Наближені оцінки індексів розраховуються як
або 100%, (4.1.4)
де = та (4.1.5)
Якщо відомі оцінки тренду і сезонної компоненти у адитивній моделі, то можна оцінити точніше:
=. (4.1.6)
Останнє говорить про можливості оцінювання рівня сезонності незалежно від того, яка розглядається модель: адитивна або мультиплікативна. Недоліком цього підходу є те, що він не враховує наявність випадкових коливань і тенденцію зміни середньорічного рівня й сезонної хвилі.
Метод декомпозиції часового ряду. Загальна процедура методу для адитивної або мультиплікативної моделей майже однакова. Спочатку виявляють та прогнозують кожну компоненту окремо (етап декомпозиції), а потім отримують загальний прогноз шляхом певного об’єднання отриманих результатів.
Побудова прогнозної адитивної або мультиплікативної тренд-сезонної моделі здійснюється за наступним алгоритмом.
1.Часовий ряд згладжується за методом ковзної середньої.
- Розраховуються різниці між вхідними даними й центрованими середніми, тобто відхилення, які характеризують сезонний чинник: .
- Розраховуються оцінки сезонної компоненти . Для цього знаходяться середні її значення для кожного періоду j:
, j=1,2,…,m; (4.1.7)
і середнє сезонне значення :
. (4.1.8)
При цьому припускається, що сезонні впливи за весь річний цикл гасять один одного, тобто для адитивної моделі і для мультиплікативної моделі. Якщо ці умови не виконуються, то середні оцінки сезонної компоненти () виправляються.
Для адитивної моделі відкоригована оцінка сезонної компоненти вимірюється у абсолютних величинах і дорівнює , .
Для мультиплікативної моделі це значення відносне – , .
- Вилученням сезонної компоненти з початкового часового ряду, одержується десезоналізований ряд.
- Аналітичне згладжування десезоналізованого ряду і одержання оцінок тренду .
- Розрахунок невипадкової складової для адитивної моделі або мультиплікативної моделі .
- Розрахунок абсолютних або відносних похибок та перевірка адекватності моделі.
- Розрахунок прогнозів.
Детальніше побудову кожної із моделей розглянемо на прикладах.
► Приклад 4.1.1. Побудувати прогноз ВВП на 2002 рік, користуючись декомпозиційним аналізом часових рядів. Оцінити ймовірність прогнозу.
В табл. 4.1.1 гр.3 досліджувалась поведінка ВВП на протязі семи років. Графічний аналіз динаміки ВВП (рис.1.2.2) вказує на наявність лінійного сезонно-адитивного або мультиплікативного тренду. Розрахуємо його компоненти.
Спочатку розглянемо адитивну модель .
Крок 1. Вирівнюємо початкові рівні ряду методом ковзної середньої з вікном згладжування 4 (згладжування ефекту квартального впливу на тенденцію ряду). Узгодимо згладжені значення із фактичними моментами часу, для чого знайдемо середні значення з двох послідовних ковзних середніх – центровані ковзні середні (гр.4 табл.4.1.1).
Крок 2. Знайдемо оцінки сезонної хвилі для кожного кварталу. Для цього шляхом віднімання від рівнів фактичного ряду () центрованих ковзних середніх () розрахуємо сезонну й випадкову компоненти (гр.5 табл. 4.1.1) і за їх значеннями проведемо в допоміжній таблиці 4.1.2. виділення сезонної складової за формулами (4.1.7 – 4.1.8). В моделях із сезонною компонентою припускається, що сезонні впливи за кожний річний період взаємо погашаються. У адитивній моделі це виражається у тому, що сума значень сезонної компоненти по всіх кварталах повинна дорівнювати нулю. Для даної моделі маємо: -4082,96-2266,1+3202,15+2686,04=-460,88.
Визначимо коефіцієнт коригування: =-460,88/4=-115,22.
Розрахуємо скориговані оцінки сезонної компоненти як різницю між її середньою оцінкою та коефіцієнтом коригування: . Оцінки зведені в табл. 4.1.1 гр.6.
Крок 3. Вилучимо вплив сезонної компоненти з ряду за формулою (гр.7 табл. 4.1.1).
Крок 4. Визначимо оцінку тренду . Для цього проведемо аналітичне згладжування ряду за допомогою лінійного тренду. Остаточно отримаємо:
(4.1.9)
Підставляючи у рівняння (4.1.9) значення знайдемо теоретичні рівні тренду як для кожного заданого моменту часу, так і для прогнозного періоду упередження (гр.8 табл. 4.1.1).
Таблиця 4.1.1
Розрахунок оцінок компонент адитивної моделі декомпозиції часового ряду.
| Рік,
квартал |
№ кварталу,
t |
ВВП, | Центрована ковзна середня | Сезонна та випадкова компоненти | Оцінка сезонної компоненти | ||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1995 кв1 | 1 | 8318,00 | – | – | -3967,74 | 12285,74 | 9701,04 | 5733,30 | 1635,51 |
| кв2 | 2 | 10694,00 | – | – | -2150,89 | 12844,89 | 11209,38 | 9058,49 | 66,92 |
| кв3 | 3 | 16102,00 | 14675,25 | 1426,75 | 3317,36 | 12784,64 | 12717,72 | 16035,08 | 2374,68 |
| кв4 | 4 | 19402,00 | 16618,13 | 2783,88 | 2801,26 | 16600,74 | 14226,05 | 17027,32 | 4921,35 |
| 1996 кв1 | 5 | 16688,00 | 18315,75 | -1627,75 | -3967,74 | 20655,74 | 15734,39 | 11766,65 | 2775,15 |
| кв2 | 6 | 17867,00 | 19748,25 | -1881,25 | -2150,89 | 20017,89 | 17242,73 | 15091,85 | 441,57 |
| кв3 | 7 | 22510,00 | 20634,75 | 1875,25 | 3317,36 | 19192,64 | 18751,07 | 22068,43 | 1393,33 |
| кв4 | 8 | 24454,00 | 21217,00 | 3237,00 | 2801,26 | 21652,74 | 20259,41 | 23060,67 | 927,99 |
| 1997 кв1 | 9 | 18728,00 | 21990,00 | -3262,00 | -3967,74 | 22695,74 | 21767,75 | 17800,01 | -640,20 |
| кв2 | 10 | 20485,00 | 22888,50 | -2403,50 | -2150,89 | 22635,89 | 23276,08 | 21125,20 | -2025,79 |
| кв3 | 11 | 26076,00 | 23623,13 | 2452,88 | 3317,36 | 22758,64 | 24784,42 | 28101,79 | -1018,02 |
| кв4 | 12 | 28076,00 | 24274,38 | 3801,63 | 2801,26 | 25274,74 | 26292,76 | 29094,02 | -2850,36 |
| 1998 кв1 | 13 | 20983,00 | 25073,75 | -4090,75 | -3967,74 | 24950,74 | 27801,10 | 23833,36 | -3718,55 |
| кв2 | 14 | 23440,00 | 25735,50 | -2295,50 | -2150,89 | 25590,89 | 29309,44 | 27158,55 | -4619,14 |
| кв3 | 15 | 29516,00 | 26504,88 | 3011,13 | 3317,36 | 26198,64 | 30817,78 | 34135,14 | -5197,38 |
| кв4 | 16 | 29930,00 | 27828,88 | 2101,13 | 2801,26 | 27128,74 | 32326,11 | 35127,38 | -4582,71 |
| 1999 кв1 | 17 | 25284,00 | 29693,00 | -4409,00 | -3967,74 | 29251,74 | 33834,45 | 29866,71 | -3460,91 |
| 2кв | 18 | 29731,00 | 31690,63 | -1959,63 | -2150,89 | 31881,89 | 35342,79 | 33191,91 | -2030,49 |
| 3кв | 19 | 38138,00 | 33580,88 | 4557,13 | 3317,36 | 34820,64 | 36851,13 | 40168,49 | -3871,73 |
| 4кв | 20 | 37289,00 | 35692,38 | 1596,63 | 2801,26 | 34487,74 | 38359,47 | 41160,73 | -2853,07 |
| 2000 кв1 | 21 | 33047,00 | 38263,38 | -5216,38 | -3967,74 | 37014,74 | 39867,81 | 35900,07 | -365,26 |
| 2кв | 22 | 38860,00 | 41105,38 | -2245,38 | -2150,89 | 41010,89 | 41376,14 | 39225,26 | 3375,15 |
| 3кв | 23 | 49577,00 | 43687,25 | 5889,75 | 3317,36 | 46259,64 | 42884,48 | 46201,85 | 1391,92 |
| 4кв | 24 | 48586,00 | 45990,00 | 2596,00 | 2801,26 | 45784,74 | 44392,82 | 47194,08 | 471,58 |
| 2001 кв1 | 25 | 42405,00 | 48296,88 | -5891,88 | -3967,74 | 46372,74 | 45901,16 | 41933,42 | 2665,39 |
| 2кв | 26 | 47924,00 | 50735,38 | -2811,38 | -2150,89 | 50074,89 | 47409,50 | 45258,61 | 6732,80 |
| 3кв | 27 | 58968,00 | – | 3317,36 | 55650,64 | 48917,84 | 52235,20 | 5475,57 | |
| 4кв | 28 | 58703,00 | – | 2801,26 | 55901,74 | 50426,17 | 53227,43 | 0,00 | |
| 2002 кв1 | 29 | 47966,77 | |||||||
| 2кв | 30 | 51291,97 | ПРОГНОЗ | ||||||
| 3кв | 31 | 58268,55 | |||||||
| 4кв | 32 | 10993,96 |
Таблиця 4.1.2.
|
|
1 | 2 | 3 | 4 | Середньо сезонне значення, | Коригуючий коефіцієнт, |
| 1995 | – | – | 1426,75 | 2783,88 | ||
| 1996 | -1627,75 | -1881,25 | 1875,25 | 3237,00 | ||
| 1997 | -3262,00 | -2403,50 | 2452,88 | 3801,63 | ||
| 1998 | -4090,75 | -2295,50 | 3011,13 | 2101,13 | ||
| 1999 | -4409,00 | -1959,63 | 4557,13 | 1596,63 | ||
| 2000 | -5216,38 | -2245,38 | 5889,75 | 2596,00 | ||
| 2001 | -5891,88 | -2811,38 | – | – | ||
| Підсумок за j-й квартал | -24497,75 | -13596,63 | 19212,88 | 16116,25 | ||
| Середня оцінка сезонної компоненти для j-го кварталу, | -4082,96 | -2266,10 | 3202,15 | 2686,04 | -460,88 | -115,22 |
| Скоригована оцінка сезонної компоненти, | -3967,74 | -2150,89 | 3317,36 | 2801,26 | 0,00 |
Крок 5. Знайдемо теоретичні рівні ряду за формулою (гр.9 табл. 4.1.1).
Крок 6. Розрахунок похибок робиться за формулою . Їх значення наведені у гр.10 табл. 4.1.1 Щоб визначити, наскільки точно модель що розглядається згладжує попередні дані, застосуємо два показники: середнє абсолютне відхилення (), корінь із середньоквадратичної похибки ().
2659,54; 3174,13.
В даному випадку складає усього 11% від середнього вибіркового значення ВВП, що говорить задовільну точність прогнозної моделі.
Крок 7. Прогнозування за адитивною моделлю. Прогнозні значення за адитивною моделлю розраховуються за формулою
(за квартал ), (4.1.10)
де тренд розраховується за рівнянням , коли дорівнює прогнозованим кварталам (), а оцінки сезонної компоненти не змінюються. Оцінки прогнозних значень ВВП на чотири квартали 2002 року наведені у табл. 4.1.1 гр.4.
Не слід забувати: чим більш віддаленим є період упередження, тим прогноз менш переконливий. В даному випадку ми припускаємо, що тенденція, виявлена за ретроспективними даними, розповсюджується і на майбутній період. Для порівняно невеликих періодів упередження таке припущення може справді бути реальним, однак воно стає менш імовірним, якщо прогноз складається на віддалену перспективу.
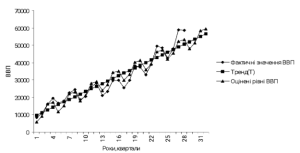
Рис.4.1.2 . Графічний аналіз динаміки ВВП за адитивною моделлю.
Розглянемо мультиплікативну модель часового ряду ВВП: .
Крок 1. Вирівнювання початкових рівнів ряду. По суті ця процедура не відрізняється від тієї, що була застосована для адитивної моделі. Так само обчислюються центровані ковзні середні згладженого ряду (гр.4 табл. 4.1.3).
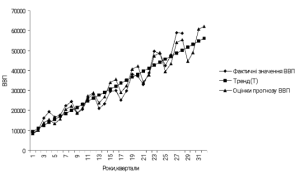
Рис.4.1.3 . Графічний аналіз динаміки ВВП за мультиплікативною моделлю.
Крок 2. Знайдемо сезонну й випадкову компоненти для кожного кварталу. Для цього розділимо фактичні рівні ряду () на центровані ковзні середні () (гр.5 табл.4.1.3). Використаємо ці значення для розрахунку відкоригованої сезонної компоненти для чого побудуємо допоміжну таблицю 4.1.4 Оскільки значення сезонної компоненти – це частки, а кількість сезонів у році дорівнює чотирьом, необхідно, щоб сума значень сезонних компонент по усіх кварталах теж дорівнювала чотирьом. Якщо ця сума не дорівнює чотирьом, то значення сезонної компоненти виправляються. Наприклад, маємо середнє сезонне значення сезонної компоненти, що дорівнює 3,44.
Визначимо коефіцієнт коригування: = 4/3,44 = 1,16.
Розрахуємо скориговані оцінки сезонної компоненти як добуток середніх квартальних оцінок на коефіцієнт коригування: . Оцінки зведені в табл.4.1.3 гр.6. Як показують оцінки, в результаті сезонних впливів ВВП в першому кварталі збільшуються на 9,6%, в третьому – на 19,4%, в четвертому відповідно на 13,5%. В першому кварталі спостерігається зменшення бюджетних видатків, яке становить 55,1% від відповідних значень тренду. В моделях із сезонною компонентою припускається, що сезонні впливи за весь річний цикл взаємо погашаються.
Крок 3. Вилучимо вплив сезонної компоненти з ряду за формулою (гр.7 табл.4.1.3).
Крок 4. Визначимо оцінку тренду . Для цього проведемо аналітичне згладжування ряду за допомогою лінійного тренду. Остаточно отримаємо:
(4.1.11)
Підставляючи у рівняння (4.1.11) значення знайдемо теоретичні рівні тренду як для кожного заданого моменту часу, так і для прогнозного періоду упередження (гр.8 табл.4.1.3).
Таблиця 4.1.3
Розрахунок оцінок компонент адитивної моделі декомпозиції часового ряду.
| Рік,
квартал |
№ кварталу,
t |
ВВП, | Центрована ковзна середня | Сезонна та випадкова компоненти | Оцінка сезонної компоненти | ||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1995 кв1 | 1 | 8318,00 | – | – | 0,86 | 9635,34 | 9546,13 | 8240,99 | 1,01 |
| 2 | 2 | 10694,00 | – | – | 0,92 | 11614,16 | 11052,68 | 10177,00 | 1,05 |
| кв3 | 3 | 16102,00 | 14675,25 | 1,10 | 1,11 | 14508,15 | 12559,22 | 13938,97 | 1,16 |
| кв4 | 4 | 19402,00 | 16618,13 | 1,17 | 1,11 | 17541,10 | 14065,77 | 15557,98 | 1,25 |
| 1996 кв1 | 5 | 16688,00 | 18315,75 | 0,91 | 0,86 | 19330,92 | 15572,31 | 13443,27 | 1,24 |
| кв2 | 6 | 17867,00 | 19748,25 | 0,90 | 0,92 | 19404,36 | 17078,86 | 15725,74 | 1,14 |
| кв3 | 7 | 22510,00 | 20634,75 | 1,09 | 1,11 | 20281,85 | 18585,40 | 20627,18 | 1,09 |
| кв4 | 8 | 24454,00 | 21217,00 | 1,15 | 1,11 | 22108,54 | 20091,95 | 22223,47 | 1,10 |
| 1997 кв1 | 9 | 18728,00 | 21990,00 | 0,85 | 0,86 | 21694,00 | 21598,49 | 18645,55 | 1,00 |
| кв2 | 10 | 20485,00 | 22888,50 | 0,89 | 0,92 | 22247,63 | 23105,04 | 21274,48 | 0,96 |
| кв3 | 11 | 26076,00 | 23623,13 | 1,10 | 1,11 | 23494,87 | 24611,58 | 27315,39 | 0,95 |
| кв4 | 12 | 28076,00 | 24274,38 | 1,16 | 1,11 | 25383,15 | 26118,13 | 28888,96 | 0,97 |
| 1998 кв1 | 13 | 20983,00 | 25073,75 | 0,84 | 0,86 | 24306,13 | 27624,67 | 23847,84 | 0,88 |
| кв2 | 14 | 23440,00 | 25735,50 | 0,91 | 0,92 | 25456,89 | 29131,22 | 26823,22 | 0,87 |
| кв3 | 15 | 29516,00 | 26504,88 | 1,11 | 1,11 | 26594,36 | 30637,77 | 34003,61 | 0,87 |
| кв4 | 16 | 29930,00 | 27828,88 | 1,08 | 1,11 | 27059,32 | 32144,31 | 35554,44 | 0,84 |
| 1999 кв1 | 17 | 25284,00 | 29693,00 | 0,85 | 0,86 | 29288,29 | 33650,86 | 29050,12 | 0,87 |
| 2кв | 18 | 29731,00 | 31690,63 | 0,94 | 0,92 | 32289,20 | 35157,40 | 32371,96 | 0,92 |
| 3кв | 19 | 38138,00 | 33580,88 | 1,14 | 1,11 | 34362,92 | 36663,95 | 40691,82 | 0,94 |
| 4кв | 20 | 37289,00 | 35692,38 | 1,04 | 1,11 | 33712,50 | 38170,49 | 42219,93 | 0,88 |
| 2000 кв1 | 21 | 33047,00 | 38263,38 | 0,86 | 0,86 | 38280,73 | 39677,04 | 34252,40 | 0,96 |
| 2кв | 22 | 38860,00 | 41105,38 | 0,95 | 0,92 | 42203,70 | 41183,58 | 37920,70 | 1,02 |
| 3кв | 23 | 49577,00 | 43687,25 | 1,13 | 1,11 | 44669,63 | 42690,13 | 47380,03 | 1,05 |
| 4кв | 24 | 48586,00 | 45990,00 | 1,06 | 1,11 | 43925,97 | 44196,67 | 48885,42 | 0,99 |
| 2001 кв1 | 25 | 42405,00 | 48296,88 | 0,88 | 0,86 | 49120,78 | 45703,22 | 39454,69 | 1,07 |
| 2кв | 26 | 47924,00 | 50735,38 | 0,94 | 0,92 | 52047,61 | 47209,76 | 43469,44 | 1,10 |
| 3кв | 27 | 58968,00 | – | – | 1,11 | 53131,06 | 48716,31 | 54068,24 | 1,09 |
| 4кв | 28 | 58703,00 | – | – | 1,11 | 53072,62 | 50222,85 | 55550,91 | 1,01 |
| 2002 кв1 | 29 | 44656,97 | |||||||
| 2кв | 30 | 49018,18 | ПРОГНОЗ | ||||||
| 3кв | 31 | 60756,45 | |||||||
| 4кв | 32 | 62216,39 |
Таблиця 4.1.4
|
|
1 | 2 | 3 | 4 | Середнє сезонне значення, | Коригуючий коефіцієнт, |
| 1995 | 1,10 | 1,17 | ||||
| 1996 | 0,91 | 0,90 | 1,09 | 1,15 | ||
| 1997 | 0,85 | 0,89 | 1,10 | 1,16 | ||
| 1998 | 0,84 | 0,91 | 1,11 | 1,08 | ||
| 1999 | 0,85 | 0,94 | 1,14 | 1,04 | ||
| 2000 | 0,86 | 0,95 | 1,13 | 1,06 | ||
| 2001 | 0,88 | 0,94 | 0,00 | 0,00 | ||
| Підсумок за j-й квартал | 5,19 | 5,54 | 6,68 | 6,65 | ||
| Середня оцінка сезонної компоненти для j-го кварталу, | 0,74 | 0,79 | 0,95 | 0,95 | 3,44 | 1,16 |
| Скоригована оцінка сезонної компоненти, | 0,86 | 0,92 | 1,11 | 1,11 | 4,00 |
Крок 5. Знайдемо теоретичні рівні ряду за формулою (гр.9 табл.2.4.3).
Крок 6. Розрахунок оцінок похибок робиться за формулою . Їх значення наведені у гр.10 табл.2.4.3
1,01; 1,02.
В даному випадку складає усього 0,003% від середнього вибіркового значення ВВП, що говорить про дуже високу точність прогнозної моделі.
Оцінки прогнозних значень ВВП на чотири квартали 2002 року наведені у табл.2.4.3 гр.4. ►
Ітераційні методи фільтрації сезонної компоненти. При виділенні (фільтрації) компонент часового ряду за допомогою тих чи інших методів неминуче постає питання про «чистоту» фільтрації, тобто питання про ступінь близькості оцінок і їх справжнім значенням , . Слід зазначити, що жоден з відомих методів не забезпечує необхідну ступінь чистоти фільтрації для часових рядів різної структури.
Ітераційні методи фільтрації складових часового ряду з’явились у свій час як результат признання неможливості виділення компонент ряду прямими методами. Основна ідея ітераційних процедур полягає у багаторазовому застосуванні простої ковзної середньої:
(4.1.12)
і одночасного оцінювання сезонної компоненти в кожному циклі. При цьому перехід від одного кроку ітераційної процедури до іншого може супроводжуватися зміною параметрів ковзної середньої. Якщо формулу для ковзної середньої записати у вигляді
, , (4.1.13)
то при переході від однієї ітерації до іншої може відбуватися зміна довжини ділянки ковзання і закону зміни вагових коефіцієнтів . В деяких ітераційних методах, окрім того, використовується регресія (як правило, лінійна) вхідного ряду на перетворений на першому кроці ряд .
Ітераційні методи відзначаються простотою і задовільною «чистотою» фільтрації компонент ряду. Однак усім їм притаманний суттєвий недолік – застосування ковзної середньої приводить до втрати частини інформації на кінцях часового ряду. Розглянемо ітераційний метод Четверикова, який дозволяє виключити вплив сезонних хвиль змінної структури. З іншими ітераційними методами можна ознайомитися за [9].
Метод Четверикова. Алгоритм застосування методу наступний.
Крок перший. Емпіричний ряд вирівнюється ковзною середньою (4.1.12) з періодом ковзання m, тобто беруться (m+1) членів вхідного ряду. Вага першого і останнього членів ряду ділиться на 2, тобто: == 1/2. членів ряду, що випали с обох його кінців або поновлюються екстраполюванням згладженого ряду, або залишаються незайманими у подальшій роботі. Формується ряд попередньої оцінки тренду і відхилення емпіричного ряду від згладженого
або , (4.1.14)
Крок другий. Для кожного і-го року розраховується – оцінка середньоквадратичного відхилення, на яку діляться потім окремі місячні (квартальні) відхилення відповідного року:
, (4.1.15)
де . (4.1.16)
Крок третій. З «нормованих» таким шляхом відхилень розраховується попередня середня сезонна хвиля:
. (4.1.17)
Крок четвертий. Середня попередньо знайдена сезонна хвиля помножується на середньоквадратичне відхилення кожного року і віднімається від емпіричного ряду:
. (4.1.18)
Крок п’ятий. Отриманий таким чином ряд, з виключеною попередньою сезонною хвилею, знов згладжується ковзною середньою (для місячних даних за п’ятьма або семи точками в залежності від інтенсивності дрібних кон’юнктурних коливань і тривалості більш великих). В результаті одержується нова оцінка тренду .
Крок шостий. Відхилення емпіричного ряду від вирівняного ряду , одержаного на кроці 5
= – , (4.1.19)
знов підлягають аналогічній обробці за кроками 2 і 3 для виявлення остаточної середньої сезонної хвилі.
Крок сьомий. Видалення остаточної сезонної хвилі виконується після множення середньої сезонної хвилі на КНi – коефіцієнт напруженості сезонної хвилі:
, (4.1.20)
де – згладжені значення ряду, – розраховані випадкові залишки: =.
► Приклад 4.1.3. Застосуємо метод Четверикова для виділення компонент часового ряду, наведеного в таблиці 4.1.1.
- Згладимо часовий ряд ковзною середньою із періодом згладжування =4. Отриману попередню оцінку тренду віднімаємо від початкового ряду: або , .
- Для кожного року (за рядком) розраховуємо оцінку середньоквадратичного відхилення величини , використовуючи формулу (4.1.16). Значення величин наведені в табл. 4.1.5. У розрахунку враховувалися тільки два останніх квартали першого року: , а у розрахунку – два перших квартали сьомого року.
Таблиця 4.1.5
| Рік | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 3272,08 | 3341,582 | 4585,675461 | 4477,209 | 5159,432 | 6477,15 | 6882,067 |
Ділимо окремі значення кожного кварталу з таблиці 2.4.1 на відхилення відповідного року: . Результат заносимо у табл.4.1.6.
Нормований залишковий ряд. Таблиця 4.1.6
| Роки | 1 | 2 | 3 | 4 |
| 1 | – | – | 0,436 | 0,851 |
| 2 | -0,487 | -0,563 | 0,561 | 0,969 |
| 3 | -0,711 | -0,524 | 0,535 | 0,829 |
| 4 | -0,914 | -0,513 | 0,673 | 0,469 |
| 5 | -0,855 | -0,378 | 0,883 | 0,309 |
| 6 | -0,805 | -0,347 | 0,909 | 0,401 |
| 7 | -0,856 | -0,409 | – | – |
| -0,771 | -0,456 | 0,666207 | 0,638012 |
Останній рядок табл.4.1.6 є попередніми значеннями середньої сезонної хвилі: .
- Знайдену у п.2 попередню середню сезонну хвилю помножимо на оцінку середньоквадратичного відхилення кожного року і віднімемо від початкового ряду: . В результаті отримуємо ряд без попередньої сезонної хвилі (табл.4.1.7).
Ряд без попередньої сезонної хвилі (). Таблиця 4.1.7
| Роки | 1 | 2 | 3 | 4 |
| 1 | – | – | 14675,25 | 16618,12 |
| 2 | 18315,75 | 19748,25 | 20634,75 | 21217 |
| 3 | 21990 | 22888,5 | 23623,12 | 24274,37 |
| 4 | 25073,75 | 25735,5 | 26504,87 | 27828,87 |
| 5 | 29693 | 31690,63 | 33580,87 | 35692,37 |
| 6 | 38263,38 | 41105,38 | 43687,25 | 45990 |
| 7 | 48296,88 | 50735,38 | – | – |
| -0,767 | -0,454 | 0,722784 | 0,578174 |
- Часовий ряд, з виключеною попередньою сезонною хвилею, знов згладжується ковзною середньою третього порядку і одержуємо нову оцінку тренду . Розраховуємо відхилення емпіричного ряду від вирівняного ряду : =–. (табл.4.1.8).
=–. Таблиця 4.1.8
| Роки | 1 | 2 | 3 | 4 |
| 1 | – | – | – | – |
| 2 | -1396,28 | -1537,08 | 2071,781 | 3163,969 |
| 3 | -3328,11 | -2326,83 | 2496,534 | 3755,19 |
| 4 | -4053,9 | -2401,44 | 2652,846 | 1745,049 |
| 5 | -4529,84 | -1950,28 | 4402,485 | 1305,344 |
| 6 | -5376,8 | -2114,3 | 6061,31 | 2612,373 |
| 7 | -1396,28 | -1537,08 | 2071,781 | 3163,969 |
- Одержані значення відхилень знов перераховуємо за п.2 для виявлення нових значень сезонної хвилі. Одержуємо наступні значення:
| Квартали | 1 | 2 | 3 | 4 |
| -0,767 | -0,454 | 0,722784 | 0,578174 |
Порівнюючи значення коефіцієнтів сезонної хвилі, одержаних на першій та другій ітераціях, можна зробити висновок, що вони незначно відрізняються один від одного.
- Розраховуємо коефіцієнт напруженості сезонної хвилі у наступному порядку: розраховуємо значення залишкової компоненти: =, значення яких наведені в табл. 4.1.9, і, використовуючи співвідношення (4.1.20), розраховуємо величини коефіцієнту напруженості для кожного року окрім першого й останнього (для першого й останнього років коефіцієнт напруженості не розраховується через те, що після повторного згладжування у них не залишилося спостережень.
=–. Таблиця 4.1.9
| Роки | 1 | 2 | 3 | 4 |
| 1 | – | – | – | – |
| 2 | -1395,513246 | -1536,62 | 2071,058 | 3163,391 |
| 3 | -3327,341996 | -2326,37 | 2495,811 | 3754,612 |
| 4 | -4053,136996 | -2400,98 | 2652,123 | 1744,471 |
| 5 | -4529,075746 | -1949,83 | 4401,762 | 1304,766 |
| 6 | -5376,030746 | -2113,85 | 6060,587 | 2611,794 |
| 7 | – | – | – | – |
Одержуємо наступні значення коефіцієнтів напруженості сезонної хвилі:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| – | 1838,548 | 517,562 | -1750,23 | -282,272 | 983,0286 | – |
- Використовуючи коефіцієнти напруженості сезонної хвилі розраховуємо остаточні значення сезонної компоненти часового ряду (табл..4.1.10):
=–. Таблиця 4.1.10
| Роки | 1 | 2 | 3 | 4 |
| 1 | – | – | – | – |
| 2 | -1409,72 | -834,132 | 1328,874 | 1063,001 |
| 3 | -396,843 | -234,813 | 374,0857 | 299,2409 |
| 4 | 1341,997 | 794,0626 | -1265,04 | -1011,94 |
| 5 | 216,4334 | 128,0641 | -204,022 | -163,202 |
| 6 | -753,742 | -445,991 | 710,5176 | 568,3616 |
| 7 | – | – | – | – |
4.2. Моделі прогнозування сезонних процесів. В основі сезонних моделей прогнозування лежать їх несезонні аналоги, які доповнені засобами відображення сезонних коливань. Сезонні моделі здатні відображати як відносно постійну сезонну хвилю, так і ту, що змінюється динамічно в залежності від тренду. Перша форма відноситься до класу адитивних, друга – до класу мультиплікативних моделей.
Моделювання сезонності з використанням множинної регресії. Множинна регресія може бути пристосована для одночасного оцінювання тренду та сезонного фактора. Наприклад, модель, що враховує тренд і сезонність можна записати у вигляді
, (4.2.1)
де – тренд;
– сезонний фактор;
– випадкова компонента;
– сезонні фіктивні змінні, які приймають значення 1 в певному кварталі і 0 – для решти кварталів.
Логарифм функції (4.2.1) дає тренд-сезонну модель з лінійними параметрами
, (4.2.2)
Розглянемо, як відображається процес розкладу сезонного часового ряду за допомогою адаптивних моделей.
Метод Хольта-Уінтерса. Цей метод, на відміну від методу Хольта, окрім лінійного тренду включає, ще й сезонну компоненту.
Прогноз на τ кроків вперед для адитивної форми моделі будується за формулою:
, (4.2.3)
де s – коефіцієнт сезонності;
– період сезонного циклу (наприклад, за квартальними даними =4). Розрахунок параметрів моделі виконують за співвідношеннями:
, (4.2.4)
, (4.2.5)
, (4.2.6)
де – параметри згладжування (адаптації), ().
Мультиплікативна модель аналогічна адитивній моделі з тією лише різницею, що розраховані за лінійною моделлю прогнозні значення коригують шляхом їх множення на сезонні коефіцієнти. Прогноз на τ кроків розраховується за формулою:
, (4.2.7)
а розрахунок параметрів робиться за співвідношеннями:
, (4.2.8)
, (4.2.9)
. (4.2.10)
Для несезонних часових рядів обчислювальні формули спрощують за рахунок виключення сезонної компоненти. При відносно постійній амплітуді сезонної хвилі доцільно використовувати адитивну модель, при її зміні у відповідності із тенденцією середнього рівня – мультиплікативну. Зазначимо, що моделі мішаного типу іноді дають точніший результат, але погано тлумачаться змістовно. Практика показує, що у випадку, коли сезонні коливання процесу великі і не дуже стабільні, мультиплікативна модель дає погані результати.
В процесі побудови моделі виконується числова оптимізація параметрів адаптації у межах [0; 1].
Метод Тейла – Вейджа. Даний метод формально пристосований до будь-яких часових рядів, однак найкращі результати він дає лише тоді, коли показник, що досліджується, відповідає стохастичному процесу Тейла-Вейджа, тобто тенденція описується експоненціальним трендом із мультиплікативно врахованою сезонністю (у цьому зв’язку особливо важливим вважається етап ідентифікації, коли на основі автокореляційної функції різницевого ряду другого порядку досліджуються властивості процесу). Метод застосовує адитивну модель, обчислювання за якою відносно прості. Тому перед використанням адитивної моделі значення рівнів часового ряду замінюють їх логарифмами і тим самим перетворюють експоненціальний тренд в лінійний і одночасно – мультиплікативну сезонність в адитивну. В результаті адитивна модель має вигляд:
, (4.2.11)
, (4.2.12)
де – рівень ряду, після вилучення сезонних коливань;
– адитивний коефіцієнт зростання;
– адитивний коефіцієнт сезонності;
– білий шум.
Прогноз, зроблений на момент часу на кроків вперед, розраховується за формулою
, (4.2.13)
де “оновлювання” коефіцієнтів на кожному наступному кроці відбувається за допомогою наступних розрахунків:
, (4.2.14)
, (4.2.15)
, (4.2.16)
де – параметри адаптації, ().
Метод Харрісона [] полягає у подвійному застосуванні процедури експоненціального згладжування Брауна. На першому кроці за допомогою ковзної середньої з вхідного ряду видаляють сезонні коливання, а потім до одержаного ряду застосовують метод простого експоненціального згладжування. Далі за відхиленнями від тренду визначають значущі гармоніки, котрі відображають сезонні коливання. На їх основі розраховують адитивні коефіцієнти сезонності:
, (4.2.17)
де аk і bk – коефіцієнти значущих гармонік k, за якими робиться підсумок.
Параметри дисконтування рівнів, що використовуються для побудови поліноміальної і коливальної складових, можуть бути різними. Їх оптимальна величина визначається методом перебору. Прогнозні оцінки формуються шляхом підсумовування прогнозних оцінок тренду, одержаних за експоненціальною моделлю і сезонною компонентою.
Застосування динамічного фільтру Лєвандовського. Очевидно, що при малих значеннях сезонних коефіцієнтів вплив випадкового коливання рівня процесу є великим, причому він тим сильніший, чим ближче значення цих коефіцієнтів до нуля. Модель у цьому випадку стає неадекватною. Запобігти такого результату можна за допомогою динамічного фільтру Лєвандовського, згідно якому величина параметру згладжування α стає (за допомогою додаткового параметра δ) залежною від суттєвості сезонних коливань. Якщо амплітуда коливань сезонних коефіцієнтів досягає чотирьох рівнів, то нове значення параметру згладжування а1, визначається як добуток α і δ. Із збільшенням амплітуди, тобто зменшенням величини h =, значення δ лінійно зменшується за співвідношенням: δ = 4h. Отже, параметр згладжування буде дорівнювати одиниці у випадку обробки звичайних часових рядів і прагнути до нуля при прогнозуванні рядів із значною сезонністю.
Авторегресійна модель має вигляд:
. (4.2.18)
Ідентифікація порядку d різницевого ряду zt, t=1,…,n’=n–d, виконується за допомогою тих самих засобів, що і для несезонних моделей.
Порядок -моделі може бути обраний таким, що дорівнює періоду сезонності, тобто р = т. У цьому випадку її розмірність співпадає з розмірністю моделі Уінтерса, параметри моделі набувають змісту індексів сезонності, але визначаються іншим способом (МНК). Кількість параметрів можна скоротити за рахунок несуттєвих за величиною впливу коефіцієнтів.
Сезонна модель авторегресії-ковзної середньої (ARIMA(p,d,q)x(P,D,Q)) містить сезонні різницеві перетворення (інтегровані ряди), авторегресії і ковзної середньої. В операторному вигляді вона набуває вигляду:
, (4.1.19)
де – оператор порядку сезонної різниці: , D – порядок інтеграції сезонного ряду m– період сезонності;;
– оператор сезонної авторегресії порядку Р;
– оператор сезонної ковзної середньої порядку Q;
р, d, визначені раніш.
Основні кроки розробки сезонної моделі збігаються із аналогічними кроками для несезонної моделі.