- Економетричні методи прогнозування.
5.1. Прогнозування на основі багатофакторних регресійних моделей. Істотна відмінність економетричних моделей від моделей часових рядів полягає у тому, що останні описують зміну досліджуваного показника як функцію його минулих тенденцій, у той час як в основі економетричних моделей лежить економічна теорія, яка встановлює залежність досліджуваного показника від зміни інших показників, у тому числі й від стану самого показника в минулому. В деяких випадках обидва типи моделей можуть бути подібними, зокрема, коли тенденція часового ряду моделюється за допомогою кривих зростання, але їх тлумачення відрізняється.
Розробка економетричних моделей з метою прогнозування для будь-якого періоду випередження починається із визначення регресійної моделі. Позначимо через ендогенні змінні, а через екзогенні змінні, де – спостереження (). Ендогенними є ті змінні, які визначаються внутрішньою структурою економічного явища, що вивчається, тобто їх величини розраховуються на основі економетричної моделі. Екзогенні змінні незалежні від внутрішньої структури економічного явища і їх величини задаються поза моделлю. Рівняння регресії характеризує кореляційну залежність ендогенної змінної від екзогенних змінних. Виділяють модель (рівняння) парної регресії
(5.1.1)
та множинної регресії
, (5.1.2)
або в матричному запису
(5.1.3)
де – вектор випадкових змінних.
Рівняння регресії передбачає, що існує тільки односторонній зв’язок між залежною (ендогенною) змінною та незалежними (екзогенними) змінними . В лінійному регресійному аналізі розглядається стохастична залежність випадкової величини від одного (парна регресія) або кількох чинників (множинна регресія), яка має наступні допущення:
; . (5.1.4)
Для множинної регресії додається ще умова лінійної незалежності стовпців матриці Х.
Якщо декілька змінних =() є функцією від =(), а , в свою чергу, є функцією від , взаємозв’язок між Y та неможливо описати за допомогою лише одного регресійного рівняння. В такому випадку переходять від регресійної моделі з одним рівнянням до регресійної моделі з багатьма рівняннями, серед яких можуть бути рівняння, які включають Y та як ендогенні і пояснюючі змінні. Модель, що описує таку взаємну залежність між змінними, називається системою одночасних або симультативних регресійних рівнянь. Системи симультативних рівнянь задаються двома формами: структурною і приведеною.
Структурна форма системи створюється в процесі побудови моделі економічного процесу при намаганні відобразити причинно-наслідковий механізм, існуючий в реальності. Вона дозволяє прослідкувати вплив величин екзогенних змінних моделі на значення ендогенних змінних. В розгорнутому вигляді структурна форма має запис:
(5.1.5)
Структурна форма системи одночасних економетричних рівнянь може бути записана у матричному вигляді
, , (5.1.6)
де – не вироджена матриця невідомих параметрів при ендогенних змінних розмірності ();
– матриця невідомих параметрів при екзогенних змінних розмірності ();
– вектор ендогенних змінних розмірності ();
– вектор екзогенних змінних розмірності ();
– вектор залишків розмірності ().
Структурна форма системи одночасних рівнянь може включати також балансові рівняння, або тотожності, які відображають балансові зв’язки між деякими змінними та об’єднують регресійні рівняння в систему.
Приведена форма моделі є результатом розв’язання рівнянь структурної форми відносно ендогенних змінних за умов, що система структурної моделі сумісна. Система (5.1.5) може бути розв’язана відносно ендогенних змінних (припускаємо, що ранг системи дорівнює m). Тоді одержимо приведену форму:
(5.1.7)
Приведену форму систем рівнянь одержують за допомогою лінійних перетворень. Кожна ендогенна змінна у приведеній формі міститься тільки в одному рівнянні і залежить, не рахуючи залишків, тільки від значень параметрів й екзогенних змінних, отже кількість усіх рівнянь в системі дорівнює кількості ендогенних змінних. Приведена форма в матричному вигляді записується, як:
або , (5.1.8)
де , ,;
– матриця коефіцієнтів приведеної форми розмірності ();
– вектор-стовпець, складений з лінійних комбінацій випадкових змінних присутніх в структурній формі рівнянь.
Рекурсивні системи є окремим випадком симультативної системи рівнянь, в яких матриця А параметрів ендогенних змінних має трикутний вигляд, а випадкові змінні не корелюють між собою. На практиці прагнуть спростити взаємозалежні системи і звести їх до рекурсивного виду. Для цього спочатку обирають ендогенну змінну, яка залежить тільки від екзогенних змінних, позначають її . Потім вибирається ендогенна змінна, яка залежить тільки від екзогенних змінних та і далі, так само, вибирається кожний наступний показник, який залежить тільки від екзогенних та вже визначених ендогенних змінних.
Лінеаризація нелінійної регресії. Зв’язок між залежною і незалежними змінними не обов’язково може бути лінійним. Використовуючи матриці показників Y та X, можна по черзі випробувати різні види залежності (див.табл.5.1.2). Для цього кожне з рівнянь регресії шляхом перетворень типу логарифмування або піднесення до ступеня зводиться до лінійної моделі. Обирається той вид зв’язку, для якого коефіцієнт детермінації () ближче до 1. В табл.5.1.1 на прикладі парної регресії розглянуті функції, які найбільш розповсюджені в практиці економічних досліджень.
Основні функції парної регресії Таблиця 5.1.1
| Модель | Перетворення | Матриці | ||
| X | Y | |||
| 1 | 2 | 3 | 4 | |
| Y=a+bX | Ні | |||
| Y=a+bX+cX2 | Ні | |||
| Y=a+b/X | Ні | |||
| Y=1/(a+bX) | Піднесення до ступеня (-1) | |||
| Y=1/(a+bexp(-X)) | Піднесення до ступеня (-1) | |||
| Y=aexp(bX) | Логарифмування | |||
| Y=a+blg(X) | Нi | |||
| Y=abхсх | Логарифмування | |||
| Y= | Логарифмування | |||
| Y=a+b/ln(x) | Ні | |||
| Y=aXb | Логарифмування | |||
| Y=a+bX+c(X)1/2 | Ні | |||
| Y=X/(a+bX) | Ні | |||
| Y=a∙exp(b/X) | Логарифмування | |||
| Y=a+bXk | Ні | |||
| Y=а+bX+cX2+…+dXk | Ні | |||
Методи оцінювання регресійних рівнянь та симультативних систем рівнянь. Рівняння множинної лінійної регресії дозволяє встановити статистичний взаємозв’язок досліджуваних показників і у випадку його значущості визначити аналітичні й прогнозовані оцінки. Оцінки параметрів знаходяться методом найменших квадратів (МНК) за умови мінімуму функціоналу:
. (5.1.9)
МНК-оцінки розраховуються за формулою:
(5.1.10)
і являються незсунутими ефективними та консистентними.
Якщо – емпірична апроксимуюча регресія, то елементи вектора =Y- називаються залишками. Аналіз залишків дозволяє зробити висновок про якість побудованого рівняння регресії. Ускладнення методів оцінювання параметрів рівняння регресії і прогнозування залежної змінної породжується невиконанням допущень регресійного аналізу [13]. Особливу увагу заслуговують такі порушення, як: мультиколінеарність, гетероскедастичність, автокореляція, незалежність між собою випадкових величин та факторів.
Якщо використовувати МНК для оцінювання параметрів рівняння, яке є складовою частиною системи одночасних структурних рівнянь (5.1.4), то одержані оцінки будуть зсуненими й неконсистентними, а статистичні тести – некоректними. Це пояснюється тим, що деякі пояснюючі змінні в правій частині рівняння є ендогенними Y і частково залежать від ε. Тим самим порушується умова класичної регресії про те, що в рівнянні регресії пояснюючі змінні не корелюють з випадковою змінною ε. Цьому можна запобігти, якщо оцінювати приведену форму моделі. Для рекурсивної системи рівнянь немає потреби в залученні складних методів оцінювання параметрів. Застосування звичайного методу МНК до кожного з рівнянь рекурсивних систем окремо приводить до консистентних оцінок параметрів.
Не завжди оцінювання приведеної форми моделі дозволяє отримати однозначні величини параметрів структурної моделі системи симультативних рівнянь. Це пов’язано із проблемою ідентифікації. Якщо система така, що визначення параметрів певного структурного рівняння в ній неможливе, то це рівняння недоототожнене і не може бути оцінене ніякими методами. Якщо існують умови, що допускають однозначну оцінку параметрів, структурне рівняння системи називається точно ототожненим. І якщо умов більше ніж потрібно для однозначної оцінки рівняння, то маємо його переототожнення.
Необхідною і достатньою умовою (умова рангу) для ототожнення певного рівняння в системі з m рівнянь є можливість утворення хоча б одного ненульового визначника порядку m-1 з коефіцієнтів змінних, які входять в систему, але відсутні в такому рівнянні. За умовою рангу загальні принципи ідентифікації окремого рівняння структурної моделі, яка складається з симультативних рівнянь, формально записуються так:
рівняння точно ототожнене, якщо ;
рівняння є переототожнене, якщо ;
рівняння недоототожнене, якщо ;
де m – кількість ендогенних змінних в системі;
mi– кількість ендогенних змінних в i-му рівнянні системи;
k – кількість екзогенних змінних в системі;
ki– кількість екзогенних змінних в i-му рівнянні.
В разі точно ототожнених рівнянь можна застосувати звичайний метод найменших квадратів (МНК). Але для цього систему одночасних структурних рівнянь треба перетворити у приведену форму.
Для оцінювання параметрів системи структурних переототожнених рівнянь застосовують спеціальні методи. Найбільш поширеними є двокроковий та трикроковий методи найменших квадратів. Якщо рівняння моделі точно ототожнені, то непрямий і двокроковий методи дають однакову оцінку параметрів моделі. Якщо рівняння будуть переототожненими, то ці оцінки будуть різними.
Суть двокрокового методу найменших квадратів (2МНК) полягає у тому, що на першому кроці для кожної ендогенної змінної будуються регресії на всі екзогенні змінні і на основі цих регресій методом найменших квадратів знаходяться теоретичні (оцінені) значення ендогенних змінних . На другому кроці в кожне структурне рівняння системи замість пояснюючих ендогенних змінних підставляється їх теоретичне значення, після чого знов застосовується МНК. Оцінки 2МНК, на відміну від звичайних МНК-оцінок, є спроможними.
Трикроковий метод найменших квадратів призначений для одночасної оцінки параметрів усіх рівнянь моделі. Суть методу полягає у тому, що спочатку застосовується двокроковий метод найменших квадратів. На основі одержаних оцінок знаходять оцінку для коваріаційної матриці похибок системи рівнянь. На третьому кроці параметри рівнянь системи переоцінюють на основі узагальненого методу найменших квадратів. Трикроковий метод найменших квадратів забезпечує кращу порівняно з двокроковим методом асимптотичну ефективність оцінок лише в тому разі, коли залишки, які входять в різні рівняння моделі, корелюють між собою.
Щоб застосувати трикроковий метод найменших квадратів на практиці необхідне виконання таких вимог:
1) усі тотожності, які входять в систему рівнянь, треба виключити, приступаючи до знаходження оцінок параметрів;
2) кожне недоототожнене рівняння також треба виключити з системи;
3) якщо система рівнянь, що залишилась, має точно ототожнені й переототожнені рівняння, то трикроковий метод оцінки доцільно застосовувати до кожної з цих груп;
4) якщо група переототожнених рівнянь має тільки одне рівняння, то трикроковий метод перетворюється на двокроковий;
5) якщо матриця коваріацій для структурних залишків блочно-діагональна, то вся процедура оцінювання на основі трикрокового методу найменших квадратів може бути застосована окремо до кожної групи рівнянь, які відповідають одному блоку.
Коефіцієнти оцінки впливовості факторів. Апарат кореляційно-регресійного аналізу дозволяє розраховувати різні оціночні коефіцієнти для визначення ступеня впливу того або іншого фактора:
– коефіцієнт граничної ефективності -го фактора – показує, на скільки одиниць свого виміру в середньому зміниться , якщо фактор хj зросте на одиницю при фіксованому стані решти факторів. Цей коефіцієнт відповідає частинній похідній за відповідною хj :
. (5.1.11)
Зазначимо, що за допомогою коефіцієнтів регресії неможливо порівняти вплив чинників на залежну змінну через розбіжність одиниць виміру і ступеня коливання.
– частинний коефіцієнт еластичності – показує, на скільки відсотків в середньому зміниться , якщо фактор хj зросте на 1% при фіксованому стані решти факторів. Коефіцієнтом еластичності користуються для економічного тлумачення нелінійних зв’язків (табл. 5.1.2). Коефіцієнт еластичності розраховується як
. (5.1.12)
Таблиця 5.1.2
| Функція | Формула коефіцієнту еластичності |
| Y=a+bx | Е=b(х/у) |
| Y=a+bx+cx2 | E= (b + 2сх)(х / у) |
| Y=a+b/x | E= b / (ax + b) |
| Y=1/(a+bx) | E= bx / (a + bx) |
| Y=1/(a+b)e-x | E= bxe-x /(a+be-x) |
| Y=aebx | E= bx |
| Y=a+bln(x) | E=b/у |
| E= | |
| Y=abx | E= |
| Y=a+b/ln(x) | E=b/(lп2(х)у) |
| Y=axb | E=b |
| Y=a+bx+c(x)1/2 | E=(b-с)(х)1/2(х/у) |
| Y=x/(a+bx) | E=а/(а+bх) |
| Y=aeb/x | E=b/х |
| Y=a+bxk | E= bkxk /(a+bxk) |
| Y=a0+a1x’+….+akxk | E= |
– бета-коефіцієнт або коефіцієнт регресії у стандартизованому вигляді використовується для усунення різниць у виміру і ступеня коливання чинників. Коефіцієнт показує, на яку частину величини середньоквадратичного відхилення змінюється середнє значення залежної змінної коли відповідна незалежна змінна збільшується на одне середньоквадратичне відхилення а решта незалежних змінних залишаються сталими:
, (5.1.13)
де – коефіцієнт регресії, який відповідає змінній ,
– оцінка середньоквадратичного відхилення j-ї пояснюючої змінної,
– оцінка середньоквадратичного відхилення залежної змінної.
– дельта- коефіцієнт – показує частку впливу кожного чинника у загальній дії усіх чинників включених в рівняння регресії. Розрахункова формула має вид:
; ; , (5.1.14)
де R2 – коефіцієнт детермінації; – коефіцієнт парної кореляції мiж j-м чинником і залежною змінною.
За коректно зробленим аналізом величини дельта-коефіцієнтів додатні, тобто усі коефіцієнти регресії мають той самий знак, що й відповідні парні коефіцієнти кореляції.
Прогнозування на основі регресійних моделей передбачає наступні етапи:
- Визначення мети дослідження. Вибір відповідної теорії, яка пояснює поведінку економічної системи. Побудова системи показників, відбір факторів, що спричиняють найбільший вплив на кожний показник та розробка логіко-інформаційної схеми прогнозу. Вибір форми зв’язку показників між собою і відібраними чинниками.
- Побудова економетричної моделі, тобто відображення теорії у вигляді рівняння регресії або системи рівнянь і тотожностей, яка пов’язує відібрані змінні. Потрібно звертати особливу увагу на випередження та запізнення впливу змінних у рівняннях, а також на змінні, які містять інформацію про перспективу на майбутнє.
- Знаходження даних про значення змінних, дотримуючись, наскільки можливо, теоретичних концепцій. Аналіз інформації. В ідеалі потрібні точні дані про всі необхідні змінні.
- Використання відповідного економетричного методу для оцінювання невідомих параметрів, які входять до рівнянь моделі.
- Перевірка якості побудованої моделі, яка включає, у першу чергу, її відповідність досліджуваному економічному процесу, а також адекватність, точність та прогнозну спроможність.
- Використання знайденої прийнятної моделі для прогнозу. На основі рівнянь з оціненими параметрами і прогнозованих екзогенних змінних робиться передбачення потрібних показників, а саме, значень ендогенних змінних. Якщо потрібний прогноз на кілька періодів вперед, його можна одержати шляхом послідовності прогнозів на один період. Знайти значення величин екзогенних змінних, від яких суттєво залежить прогноз, можна або на основі одномірної моделі часових рядів, або використовуючи інші джерела, наприклад, іншу економетричну модель або експертні методи.
Як і раніше, позначимо прогноз на період часу () через . При цьому >1 є періодом випередження, відповідно помилки прогнозу дорівнюють: . 3 огляду на те що значення помилок можуть бути як від’ємними, так і додатними, використовується поняття мінімуму середнього квадрата помилок (MSE). Відповідно, оптимальним є прогноз, при якому мінімізується середній квадрат помилок прогнозу. Тобто обирається таке прогнозне значення , при якому мінімізується . Зауважимо, що, оскільки помилка прогнозу є випадковою величиною, ми мінімізуємо математичне сподівання квадрата помилок. Мінімізація середнього квадрата помилок аналогічна прогнозному значенню , отриманому як умовне сподівання при заданих всіх спостереженнях часового ряду до періоду t, тобто = (див. 7.1).
Допустимо для побудованої моделі виконуються усі допущення лінійної регресії. Тоді за відомими значеннями факторів=() на період випередження незміщена оцінка точкового прогнозу дорівнює:
. (5.1.15)
Якість прогнозу тим вища, чим: надійніше оцінені параметрів моделі; точніше визначені значення незалежних змінних для періоду випередження прогнозу; точніше виконуються в прогнозованому періоді усі допущення лінійної регресії.
Інтервал надійності прогнозу отримаємо для математичного сподівання залежної змінної та для індивідуального значення . Дисперсії величини будуть у цих випадках різними. Оскільки, похибка прогнозу є лінійною функцією нормально-розподіленої змінної , то
дисперсія математичного сподівання прогнозу дорівнює
. (5.1.16)
Виходячи з цього, інтервал надійності математичного сподівання для рівня довіри визначається за формулою:
, (5.1.17)
де – визначається з таблиць t-розподілу;
Дисперсія похибки індивідуального прогнозу дорівнює
(5.1.18)
Відповідно, інтервал надійності для індивідуального значення визначається за формулою:
. (5.1.19)
Переваги прогнозування на базі економетричних моделей цілком визначаються розвитком обчислювальної техніки та програмних продуктів. Завдяки їх використанню можна, по-перше збільшувати розмірність моделі, розглядаючи глибші подробиці економічних зв’язків. Важливим є те, що модельні розрахунки дозволяють одержати прогнози не просто за великою кількістю показників, але при цьому показники збалансовані, не суперечать один одному, взаємопов’язані у систему.
Однак, економетричні моделі не позбавлені недоліків. Будучи зручним інструментом прогнозування, вони не розв’язують і не можуть розв’язати його принципові проблеми. Перш за все, моделі не сприяють підвищенню точності прогнозування поворотних точок розвитку. У економетричних моделях припускається, що інституції (закони, ділова практика, економічна політика тощо) залишаються незмінними у часі або їхні зміни контролюються. Вони більш придатні для екстраполяції вже встановлених тенденцій розвитку, ніж для розпізнання зміни у них. За цією причиною прогнозування економічного зростання на базі моделей можливе лише через введення зовнішніх змінних і коригувань параметрів.
Окрім того, на практиці не завжди можливо сконструювати економетричну модель. По-перше, дослідник може бути непевним відносно вибору відповідної економічної теорії. По-друге, надійні дані про значення змінних, які відносяться до даної моделі, можуть не існувати. З аналізу економічного моделювання та прогнозування зрозуміло, що побудова спроможних прогнозів вимагає не тільки коректної економічної теорії, а й правильних рішень на кожному етапі побудови прогнозу. Іншими словами, прогнози є комбінацією економічної теорії та мистецтва прогнозиста. Як наслідок, дослідження прогнозів не обов’язково може визначити, який з варіантів економічної теорії є коректним, і не завжди дає багато інформації про відмінності між економічними моделями. Може виявитись, що на точність прогнозу найбільш впливає передбачення або припущення стосовно майбутніх заходів уряду та значень екзогенних змінних.
Приклад 5.1.1. Розробити прогноз впливу державної фінансової політики на функціонування економіки країни, використовуючи модель Л. Клейна [], яка відображає залежність шести ендогенних змінних від трьох екзогенних змінних (табл. 5.1.3). Дані умовні.
Ендогенні змінні: С(t) – особисте споживання, W1(t) – заробітна плата, P(t) – прибуток, I(t) – інвестиції, K(t) – основний капітал, Y(t) – національний дохід.
Екзогенні змінні: W2 (t) – державний фонд заробітної плати, G(t) – державні замовлення, X(t) – податок на ділову активність або податок на підприємництво (складаються з податків на продаж, акцизи, податки на майно, сплата ліцензій та мита).
Вхідна інформація для розрахунків економетричної моделі. Таблиця 5.1.3
| Роки
(t) |
Y(t) |
I(t) |
G(t) |
C(t) |
X(t) |
P(t) |
W1(t) |
W2(t) |
K(t) |
| 1 | 1203,5 | 240,8 | 299,1 | 795,5 | 131,9 | 120,2 | 683,3 | 400 | 1220,8 |
| 2 | 1289,1 | 219,6 | 355 | 862 | 147,5 | 137,1 | 720,1 | 431,9 | 1440,4 |
| 3 | 1441,4 | 277,7 | 356,9 | 969 | 162,2 | 146,4 | 740 | 555 | 1718,1 |
| 4 | 1617,8 | 344,1 | 387,3 | 1057,6 | 171,2 | 150,2 | 810 | 657,6 | 2062,2 |
| 5 | 1838,2 | 416,8 | 425,2 | 1177,8 | 181,6 | 168,1 | 850,3 | 819,8 | 2479 |
| 6 | 2047,3 | 454,8 | 467,8 | 1319,8 | 195,1 | 174 | 895,5 | 977,8 | 2933,8 |
| 7 | 2203,5 | 437 | 530,3 | 1460,8 | 224,6 | 188,3 | 949,3 | lt)65,9 | 3370,8 |
| 8 | 2443,5 | 515,5 | 588,1 | 1601,2 | 261,3 | 196,2 | 1026,3 | 1221 | 3886,3 |
| 9 | 2518,4 | 447,3 | 641,7 | 1693,8 | 264,4 | 200,4 | 1180 | 1138 | 4333,6 |
| 10 | 2719,5 | 502,3 | 675 | 1831,8 | 289,6 | 222,6 | 1290,6 | 1206,3 | 4835,9 |
| 11 | 3028,5 | 664,8 | 735,9 | 1956 | 328,2 | 288,6 | 1360,6 | 1379,3 | 5500,7 |
| 12 | 3234 | 643,1 | 820,8 | 2113,7 | 343,6 | 292,1 | 1500 | 1441,9 | 6143.8 |
| 13 | 3437,1 | 665,9 | 871,2 | 2247,3 | 347,3 | 300,4 | 1685,8 | 1450,9 | 6809,7 |
| 14 | 3678,7 | 712,9 | 924,7 | 2409,1 | 368 , | 290 | 1826 | 1562,7 | 7522,6 |
| 1 | 3964,3 | 765,5 | 936,3 | 2655,2 | 392,7 | 310 | 2090 | 1564.3 | 8288,1 |
Розв’язування.
Математична модель задачі має вид:
Рівняння функціонування
Функція споживання: C(t)=f(W(t), P(t), P(t-1)) або
C(t) = а0 + а1 (W2(t) + W1(t))+ a2 P(t) + a3 P(t-1) +U1t. (1)
Функція інвестицій: I(t)=f(P(t),P(t-1),K(t-1)) або
I(t)=b0 +b1 P(t)+b2 P(t-1)+b3 K(t-1)+U2t. (2)
Функція попиту на робочу силу: W1(t)=f(Z(t), Z(t-1),T) або
W1(t)=d0+d1Z{t)+ d2Z(t-1)+ d3T+U3t , Z(t)=(Y(t)+ Х(t)- W2(t)). (3)
Тотожності
Рівняння національного доходу Y(t)=C(t)+I(t)+G(t) – X(t). (4)
Рівняння прибутку P(t)= Y(t) – W1(t) +W2(t)). (5)
Рівняння зміни капіталу K(t) = K(t-1)+I(t). (6)
Розрахунки за моделлю проводяться в чотири етапи: формування інформаційної бази, оцінювання параметрів моделі, побудова економетричних моделей зв’язку ендогенних змінних, аналіз моделі.
Інформаційна база, окрім усіх вхідних даних, передбачає формуванням додаткових блоків для лагових ендогенних змінних: Y(t-1), X(t-1), P(t-1), K(t-1), W2(t-1), Z(t-1).
Параметри структурної моделі (1-6) можна розрахувати двокроковим або трикроковим МНК, оскільки модель не містить недоототожнених рівнянь. В результаті розрахунків одержуємо наступну числову модель задачі:
Функція споживання: C(t) =36,2+ 0,81(W2(t) +0,66W1(t)+0,0095P(t)-0,42P(t-1)+U1t. (7)
Функція інвестицій: I(t)=64,7+1,648P(t)-0,32P(t-1)+0,037K(t-1)+U2t. (8)
Функція попиту на робочу силу:
W1(t)=52,62+1,06Y(t)-0,83X(t)-1,104W2(t)-0,129Z(t-1)+13,25T+U3t . (9)
Рівняння національного доходу: Y(t)=C(t)+I(t)+G(t) – X(t). (10)
Рівняння прибутку: P(t)= Y(t) – W1(t) +W2(t)). (11)
Рівняння капіталу: K(t) = K(t-1)+I(t). (12)
Якщо виразити ендогенні змінні через лагові ендогенні й екзогенні змінні та константи, рівняння (7-12) матимуть вид:
C(t)- 0,81(W2(t) -0,0095P(t) =36,2+0,66W1(t)-0,42P(t-1)+U1t. (13)
I(t)-1,648P(t)=64,7-0,32P(t-1)+0,037K(t-1)+U2t. (14)
W1(t) -1,06Y(t)=52,62-0,83X(t)-1,104W2(t)-0,129Z(t-1)+13,25T+U3t, (15)
Y(t) -C(t)- I(t) = G(t) – X(t), (16)
Y(t) -P(t)- W1(t)= W2(t), (17)
K(t) -I(t) = K(t-1). (18)
Систему (13 – 18) можна записати в загальному матричному вигляді:
АY=В, (19)
де А – матриця, складена з коефіцієнтів при шести ендогенних змінних,
Х – вектор невідомих ендогенних змінних, якому відповідає вектор-стовпець,
В – вектор вільних членів, якому відповідають співвідношення між константами, екзогенними та ендогенними лаговими змінними.
Або в чисельному вигляді:
(20)
Для розв’язування системи рівнянь (20) необхідно знайти Y=А -1*В.
В результаті одержимо:
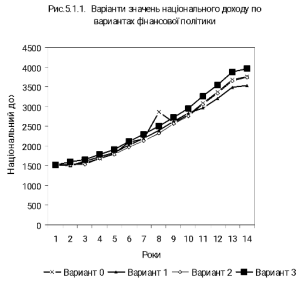
Дослідимо вплив трьох фінансових політик уряду на величину національного доходу (табл. 5.1.4). Варіанти політики на кожний рік характеризуються відповідно:
1) зниженням податку X(t) на 5%;
2) збільшенням урядового фонду заробітної плати W2(t) на 5 %;
- збільшенням урядових замовлень G(t) на 5 %.
Результати розрахунків за моделлю. Таблиця 5.1.4
| T | C(t) | I(t) | W1(t) | Y(t) | P(t) | K(t) | |||
| Варіант (0) – базовий | |||||||||
| 1 | 1048,908 | 262,2796 | 971.4021 | 1518,687 | 115,3855 | 1483,079 | |||
| 2 | 1019.739 | 306.4003 | 830.6135 | 1520,839 | 135,2262 | 1789.479 | |||
| 3 | 1030,635 | 322, 985O | 769.9422 | 1569,720 | 142,1680 | 2112,464 | |||
| 4 | 1090,010 | 356,5600 | 713,8314 | 1690,170 | 156,5388 | 2469,024 | |||
| 5 | 1140,896 | 390,4097 | 654,4602 | 1804.005 | 171,7456 | 2859.433 | |||
| 6 | 1358,669 | 414, 1272 | 861.8403 | 2107,996 | 180,2058 | 3273.560 | |||
| 7 | 1356,929 | 493,6134 | 735,7277 | 2177,343 | 220,6154 | 3.767,173 | |||
| 8 | 1510,584 | 471.9911 | 1017.717 | 2359,875 | 204,1587 | 4239,164 | |||
| 9 | 1673,220 | 527,0658 | 1155,779 | 2585,686 | 223,6069 | 4766,229 | |||
| 10 | 1767,421 | 010.9697 | 1140,526 | 2786,091 | 266,2648 | 5377,198 | |||
| 11 | 1969,857 | 633.3597 | 1364,174 | 3080.416 | 274.2530 | 6010,557 | |||
| 12 | 2196.286 | 640,8284 | 1644,174 | 3361,014 | 265,9399 | 6651,385 | |||
| 13 | 2423,221 | 698,5046 | 1831.013 | 3678,425 | 284,7124 | 7349.889 | |||
| 14 | 2464.201 | 751,9075 | 1890,551 | 3759,709 | 304.8572 | 8101.796 | |||
| Варіант (1) – щорічне зменшення податку на 5% | |||||||||
| 1 | 1048,908 | 262.2796 | 971,4021 | 1518,687 | 115.3855 | 1483,079 | |||
| 2 | 1016,982 | 284.4809 | 827,3281 | 1504,273 | 121,9455 | 1767,559 | |||
| 3 | 1080,241 | 309,986 | 825,0847 | 1614,887 | 132,2032 | 2077,545 | |||
| 4 | 1129,322 | 342.4656 | 757,8390 | 1724,487 | 146,8487 | 2419,965 | |||
| 5 | 1178,879 | 374.9634 | 696.9379 | 1836.342 | 161,6046 | 2794,863 | |||
| 6 | 1299,756 | 408,4863 | 782,9602 | 2025,142 | 176,2821 | 3203,286 | |||
| 7 | 1381,183 | 472,8060 | 764.0480 | 2193,889 | 208.8412 | 3676,106 | |||
| 8 | 1555,350 | 450,6725 | 1067.534 | 2396.543 | 191,0082 | 4126.772 | |||
| 9 | 1720,381 | 503,2695 | 1208,034 | 2623..531 | 209,1964 | 4630,069 | |||
| 10 | 1818,657 | 583,8430 | 1197,186 | 2826,600 | 250,1137 | 5213,943 | |||
| 11 | 1893,715 | 581.6225 | 1260,676 | 2969,738 | 267,1624 | 5795,572 | |||
| 12 | 2073,237 | 584,9945 | 1486,681 | 3199,532 | 261,9509 | 6380,494 | |||
| 13 | 2271,205 | 637,3594 | 1638,927 | 3483,664 | 282,0372 | 7017,849 | |||
| 14 | 2286,808 | 684,7725 | 1667.425 | 3534,820 | 303,0949 | 7702,622 | |||
| Варіант(2) – щорічне збільшення урядового фонду заробітної плати на 5% | |||||||||
| 1 | 1048.908 | 262,2796 | 971,4021 | 1518,687 | 115,3855 | 1483,079 | |||
| 2 | 1008,822 | 311,7385 | 794,0457 | 1515,261 | 138,4653 | 1794,818 | |||
| 3 | 993.5362 | 319,7791 | 698,1546 | 1529,415 | 140,7506 | 2114,579 | |||
| 4 | 1078,420 | 364,5222 | 664,7143 | 1686,542 | 161,0379 | 2479,102 | |||
| 5 | 1110,025 | 399,9937 | 577.8286 | 1782,719 | 178,2011 | 2679,093 | |||
| 6 | 1223.264 | 436,9866 | 651,8901 | 1965,951 | 194,8708 | 3316,076 | |||
| 7 | 1295,946 | 506,1168 | 616.7321 | 2128,863 | 230,0815 | 3822,185 | |||
| 8 | 1467,858 | 484,0327 | 922,241 | 2329,190 | 212,0490 | 4306,212 | |||
| 9 | 1,635,166 | 540,0360 | 1062,513 | 2560,602 | 231,4799 | 4846,246 | |||
| 10 | 1727,656 | 625,8885 | 1037,964 | 2761,245 | 275.0265 | 5472,138 | |||
| 11 | 1928.180 | 649,1963 | 1257,189 | 3054,577 | 283,3974 | 6121,336 | |||
| 12 | 2155,279 | 657,0936 | 1537,772 | 3336,273 | 275,0664 | 6768,433 | |||
| 13 | 2382,207 | 716,2516 | 1719,962 | 3655,159 | 294,3564 | 7494,681 | |||
| 14 | 2423,802 | 770,0043 | 1780,475 | 3737,406 | 314,4105 | 8264,684 | |||
| Варіант (3) – щорічне збільшення урядових замовлень на 5% | |||||||||
| 1 | 1048,908 | 262,2796 | 971,4021 | 1516,687 | 115,3855 | 1483,079 | |||
| 2 | 1079,011 | 299,0019 | 904,7668 | 1590,513 | 130,7462 | 1782,081 | |||
| 3 | 1107,473 | 314,8187 | 863,6767 | 1657,791 | 136,5150 | 2096,898 | |||
| 4 | 1175,490 | 347,4392 | 817,7704 | 1787,829 | 150,2593 | 2444,329 | |||
| 5 | 1233,973 | 386,2238 | 767,6867 | 1910,297 | 164,9110 | 2824,553 | |||
| 6 | 1364,083 | 414,6963 | 865,0857 | 2110,979 | 180,0140 | 3239,246 | |||
| 7 | 1451,200 | 480,6445 | 853,5477 | 2288,045 | 213,4973 | 3719,884 | |||
| 8 | 1632,205 | 457,7111 | 1166,102 | 2499,296 | 195,1940 | 4177,591 | |||
| 9 | 1803,357 | 511,8773 | 1313,848 | 2734,205 | 214,0571 | 4689,467 | |||
| 10 | 1907,346 | 594,1891 | 1310,744 | 2946,025 | 255,9810 | 5283,649 | |||
| 11 | 2^24,714 | 614,3844 | 1552,561 | 3257,338 | 262,8769 | 5897,984 | |||
| 12 | 2360,342 | 620,4030 | 1843,402 | 3548,295 | 253,9035 | 6518,383 | |||
| 13 | 2595,421 | 676,5427 | 2040,082 | 3874,864 | 272,0814 | 7194,922 | |||
| 14 | 2637,403 | 729,2179 | 2100,561 | 3957,081 | 292,1694 | 7924,117 | |||
Для кожного варіанта окремо розраховується величина національного доходу і вибирається той варіант, де його середня величина за 14 років є максимальною. Перш за все, за моделлю (13)-(18) розраховується базовий варіант (0 – варіант), а далі послідовно реалізуються вищезгадані три політики уряду (табл. 5.1.4).
Для кожного з варіантів розрахуємо середнє значення національного доходу Y і дисперсію S2. З даних таблиці 5.1.4 видно, що найбільше середнє значення національного доходу Y(t) відповідає третій політиці уряду – збільшення замовлень на 5 %. При цьому середній максимальний національний дохід дорівнює Y = 2548,65, але йому відповідає дисперсія S2 == 675480,5 – найбільша серед решти варіантів, включаючи й базовий. Тому, з погляду стабільності рівня національного доходу, доцільно вибрати політику уряду про зниження податку Х(і) на 5 %, тобто варіант 1. Для цього варіанту середній національний дохід дорівнює Y = 2389,438 одиниць, але дисперсія S2= 486533,2 є найменшою серед усіх варіантів.
Значення національного доходу для одержаних траєкторій Таблиця 5.1.4
| Роки | Варіант (0) | Варіант (1) | Варіант (2) | Варіант (3) |
| 1 | 1518,687 | 1518,687 | 1518,687 | 1516,678 |
| 2 | 1520,839 | 1504,273 | 1515,261 | 1590.513 |
| 3 | 1569,720 | 1614,887 | 1529,415 | 1657,791 |
| 4 | 1690,170 | 1724,487 | 1686,542 | 1787,829 |
| 5 | 1804,005 | 1836,342 | 1782,719 | 1910,297 |
| 6 | 2107,996 | 2025,142 | 1965,951 | 2110,979 |
| 7 | 2177,343 | 2193,889 | 2128,863 | 2288,045 |
| 8 | 2859,875 | 2396,543 | 2329,190 | 2499,296 |
| 9 | 2585,686 | 2623,531 | 2560,602 | . 2734,205 |
| 10 | 2786,091 | 2826,600 | 2761,245 | 2946,025 |
| 11 | 3080,416 | 2969,738 | 3054,577 | 3257,338 |
| 12 | 3361,014 | 3199,532 | 3336,273 | 3548,205 |
| 13 | 3687,425 | 3483,664 | 3655,159 | 3874,864 |
| 14 | 3759,709 | 3534,820 | 3737,406 | 3957,031 |
| ΣY | 33999,98 | 33452,14 | 33561,89 | 35681,11 |
| Yсер. | 2428,57 | 2389,438 | 2397,277 | 2548,650 |
| S2 | 591168,1 | 486533,2 | 597829,7 | 675490,5 |
5.2. Економетричне прогнозування на основі ARIMA та VAR моделей. Обговорення у попередніх розділах різноманітних методів прогнозування показало, що одномірні моделі аналізу часових рядів (,,) є атеоретичними, оскільки при їх побудові економічна теорія майже не використовується. Ці моделі прості у використанні і не потребують великих затрат. Навпаки, аналіз економетричних моделей прогнозування підкреслює роль економічної теорії. Але важливим недоліком таких моделей є велика вартість їх дослідження і, разом з тим, ненадійність структурних зв’язків, відтворюваних в моделі, через непередбачені зміни реальних економічних процесів. Для того, щоб уникнути проблем, пов’язаних з формулюванням припущень на основі певного знання економічної теорії, розроблено економетричний апарат, який дозволяє техніку одномірного прогнозування розповсюдити і на випадок декількох змінних. Одним з аргументів на користь використання одномірної моделі є те, що її можна одержати зі структурної моделі і тоді оцінена одномірна модель може забезпечити високу якість прогнозу за відносно низькою ціною. У цьому параграфі ми розглянемо деякі багатомірні узагальнення -моделей. Почнемо з прикладу.
Приклад 5.2.1. Для показу зв’язку між економетричним та суто статистичним підходами до прогнозування розглянемо приклад простої моделі економіки країни, яка задається наступними рівняннями:
де ендогенні змінні є, відповідно, реальним доходом, споживанням, інвестиціями та урядовими витратами в момент часу t. В рівняння входить минуле значення однієї ендогенної змінної, а саме, значення реального доходу в момент часу t-1, та α, β, δ, ρ, G’ є додатними сталими. Збурення εt є білим шумом, тобто для всіх t та для t ≠ s, а дисперсія – є сталою.
У загальному випадку ми можемо розв’язати систему рівнянь, одержавши рівняння приведеного вигляду, в яких кожна ендогенна змінна записана як функція від усіх екзогенних змінних та значень ендогенних змінних системи у попередні моменти часу. Отже, підставивши (2), (3) та (4) у (1), ми отримаємо рівняння для доходу у приведеному вигляді
, (5.2.1)
де та .
У (5.2.1) величина виражена через свої попередні значення, сталу та збурення. Отже, (5.2.1) є одномірним зображенням для , яке відоме як авторегресія першого порядку або -процес, оскільки виражається через своє значення у попередній момент часу. Таким чином, економічну модель можна звести до простої одномірної моделі. Якщо застосувати оператор лагів (зсуву у часі) L, визначений рівняннями можна записати (5.2.1) як
, (5.2.2)
або
. (5.2.3)
Якщо -1 < π < 1, то підстановка у (5.2.3) розкладу у геометричний ряд
дає рівняння
(5.2.4)
У (5.2.4) значення є функцією від сталої та нескінченної кількості похибок, які є білим шумом. Якщо ряд можна записати у такий спосіб, то кажуть, що це є процес рухомого середнього нескінченного порядку або . Остаточно, виразивши у (2) через С і підставивши замість та у (5.2.1), можна в результаті перетворень переписати рівняння (2) у вигляді
. (5.2.5)
Тут виражена через свої значення у попередні моменти (і, таким чином, є процесом авторегресії першого порядку або ) та значення залишків у поточний і попередній моменти часу (тобто є процесом рухомого середнього першого порядку або ). Процеси такого типу відомі як процес авторегресійного рухомого середнього або .
Цей простий приклад ілюструє, як дві ендогенні змінні структурної моделі, та , можна зобразити у вигляді одномірного часового ряду і виразити виключно у термінах їх власних минулих значень та/або випадкових похибок. Все вищесказане можна також застосувати до решти ендогенних змінних, 1 та G. Звичайно, якщо змінити модель, включивши додаткові ендогенні змінні і значення інших змінних у попередні моменти часу, то зміняться також і одномірні зображення.
-моделі є зручним інструментом коротко та середньострокового прогнозування окремих часових рядів. Однак сучасні дослідження зосереджуються на розробці апарату одночасного моделювання декількох часових рядів за допомогою системи динамічних рівнянь -процесів, що дозволяє включати та досліджувати взаємозворотні зв’язки між показниками та їх лаговими значеннями.
Системи, що складаються лише із змінних, які залежать одна від іншої, а також від лагових значень всіх змінних моделі, отримали назву (vector autoregressive) моделей. У цих моделях не намагаються відтворити реальну структуру економіки, немає поділу змінних на екзогенні та ендогенні. Тому -моделі зазвичай використовують для прогнозування, хоча за їх допомогою можна аналізувати взаємозалежність між змінними, точно встановлювати їх структуру. Якщо при аналізі моделі використовуються лагові значення деякого процесу з властивостями “білого шуму”, то такі моделі називаються (vector autoregressive moving average). Крім того, якщо замість значень часового ряду беруться послідовні різниці, то система називається (vector autoregressive integrated moving average). Якщо додати до стандартної -моделі декілька екзогенних змінних, то отримана модель називатиметься (vector autoregressive moving average with exogenous variables).
Зазначимо, що -модель є багатомірним узагальненням кількох підходів до економетричного моделювання, а саме: симультативних систем одночасних рівнянь, критики Сімса економетричних моделей [14] та багатомірних -моделей. Кожна з цих відправних точок може привести до векторних авторегресійних моделей.
Прикладом побудови простої -моделі є модель прогнозування процентних ставок (Rt) і процентної зміни грошової маси (Мt):
.
Основною відмінністю цієї моделі є симетрія змінних – обидві змінні з’являються по обидві сторони кожного рівняння. Таке подання системи рівнянь є структурною формою -моделі. Як і у випадку симультативних систем рівнянь, структурну форму -моделі завжди можна переписати у вигляді приведеної форми, тобто виразити усі ендогенні змінні тільки через предетерміновані змінні. -модель у приведеній формі називається стандартною -моделлю.
Означення стандартної -моделі. В загальному випадку, якщо досліджується т змінних, кожна з яких спостерігалася на протязі п періодів, то приведена векторна авторегресійна модель -го порядку () описується системою рівнянь
(5.2.6)
де – номер змінної,
– коефіцієнти моделі,
– векторні процеси “білого шуму”.
Для спрощення запису введемо нові позначення:
, , , , .
Тоді модель (5.2.6) приймає вигляд
, (5.2.7)
де І – одинична матриця розміру .
Використовуючи поліном від оператора зсуву, , отримуємо запис -моделі у матричному вигляді:
. (5.2.8)
При цьому припускається, що ряди стаціонарні, тобто мають постійну дисперсію та математичне сподівання, значення яких не залежать від періоду часу. У випадку нестаціонарних часових рядів їх необхідно перетворити на стаціонарні операцією різниць. Інакше, оцінені коефіцієнти моделей можуть бути хибними, а похибка регресії (estimated error) – викривленою. Випадкові величини є “білим шумом”, але корелюють між собою.
По аналогії з -процесами, які завжди можна представити у вигляді процесів ковзної середньої, вектор-авторегресійні моделі можна представити у вигляді вектор-процесів ковзної середньої. Так, -процес виду (5.2.8) можна перетворити у -процес, який у стандартному вигляді записується, як
, (5.2.9)
де – одинична матриця, а кожна матриця коефіцієнтів має вигляд
.
Практична побудова -моделі складається з наступних етапів:
- визначення порядку () моделі;
- оцінювання параметрів;
- побудова прогнозу;
- аналіз функції імпульсних відгуків (аналіз реагування на шоки) та декомпозиція дисперсії.
Визначення порядку -моделі є першим практичним етапом її побудови. Основне питання полягає у визначенні кількості рівнянь у системі, кількості лагів для кожної змінної. При включенні багатьох змінних з великою кількістю лагів систему важко оцінити та аналізувати взаємовплив змінних одна на одну. Разом з тим, невелика кількість змінних або лагів може призвести до неправильної оцінки моделі. Незважаючи на певну невизначеність стосовно параметра р, треба пам’ятати, що краще додати до моделі зайві лаги, аніж зменшити їх необхідну кількість. В останньому випадку в моделі можливе зсунення оцінок, викликане помилкою специфікації, в той час як у першому випадку можлива лише втрата деякої ефективності оцінених коефіцієнтів. На практиці обирається спочатку максимально можливе значення . Воно може обиратися декількома шляхами. Наприклад, якщо економічна інформація є квартальною, то частіше за все обирають =4 або =8. Вибір залежить також від кількості спостережень за процесом, оскільки якщо є лише декілька спостережень, то можна використовувати дуже малі значення .
Найбільш формальним критерієм вибору є АІС критерій, який для -моделі модифікується до вигляду:
, (5.2.10)
де – коваріаційна матриця залишків при застосуванні методу найменших квадратів, – детермінант коваріаційної матриці.
Тоді вибір проходить таким чином. Спочатку підраховуються послідовно значення АІС(р) для всіх , де квадратні дужки позначають цілу частину числа. За величину обирається те значення р, при якому мінімізується АІС(р) .
Ще однією можливістю вибору є застосування наступного критерію. Нехай модель має s рівнянь, кожне з яких має лагів. Всього маємо змінних, виключаючи константи. Спочатку визначимо параметри моделі і підрахуємо визначник коваріаційної матриці похибок . Зменшимо кількість лагів до величини і знайдемо відповідне значення . Після цього обраховується статистика
=. (5.2.11)
Якщо < , то обираємо модель з меншим числом лагів . На жаль, цей критерій може лише визначити, яка кількість лагів чи є кращою, і не в змозі визначити оптимальну кількість лагів. Тому для застосування цього методу необхідно перевіряти всі значення кількості лагів р від 0 до .
Оцінювання -моделей. Загальна кількість коефіцієнтів, які потрібно оцінити у -моделі виду (5.2.7), в якій присутні змінних, сягає (коефіцієнти вектора С, матриць ). Для спрощення процесу знаходження коефіцієнтів введемо позначення:
– матриця розміру коефіцієнтів моделі,
; – вектор розміру екзогенних змінних.
Тоді модель (5.2.7) запишеться як:
. (5.2.12)
Очевидно, що оцінити таку модель неважко за допомогою методу найменших квадратів, який дає консистентні та асимптотично ефективні оцінки. Оскільки існує рівнянь, то необхідно застосувати цей метод разів. Однак, зазначимо, що це можливо, оскільки кількість лагових змінних в кожному рівнянні системи однакова. Якщо це не так, то оцінка системи на основі МНК неможлива. В такому випадку -модель необхідно оцінювати методом уявно непов’язаних регресій SUR, що забезпечує ефективні оцінки.
Для оцінювання коефіцієнтів структурної форми за знайденими коефіцієнтами приведеної форми, потрібно вирішити питання ототожнення, яке формулюється у вигляді завдання певних обмежень. Так, система у структурній формі буде точно ототожненою, якщо на один з параметрів буде накладено обмеження; якщо обмеження накладено більше ніж на один параметр, система буде переототожненою.
Прогнозування на основі VAR-моделей. Завдяки VAR-моделям можна отримати одночасно прогнози багатьох взаємопов’язаних економічних показників. Звичайно, передбачення майбутніх значень часових рядів має проводитись, як і у випадку ARIMA-моделей, з мінімально можливою помилкою.
Нагадаємо, що при прогнозуванні можливі два типи помилок: пов’язані з різницею між дійсними та оціненими коефіцієнтами моделі, що використовується для прогнозу, та пов’язані з ігноруванням випадкових величин (майбутніх збурень). Класично беруть до уваги лише другий тип помилок, тому при прогнозуванні намагаються мінімізувати саме його.
Як і раніше, позначимо прогноз в період часу () через . При цьому є прогнозним періодом, або періодом випередження. Відповідно помилки прогнозу дорівнюють: . 3 огляду на те що значення помилок можуть бути як від’ємними, так і додатними, використовується поняття мінімуму середнього квадрату помилок (MSE). Відповідно, оптимальним є прогноз, при якому мінімізується середній квадрат помилок прогнозу. Тобто обирається таке прогнозне значення , при якому мінімізується . Зауважимо, що, оскільки помилка прогнозу є випадковою величиною, ми мінімізуємо математичне сподівання квадрата помилок.
Мінімізація середнього квадрату помилок аналогічна прогнозному значенню , отриманому як умовне сподівання при даних усіх спостережень часового ряду до періоду t, тобто .
Загальний принцип розрахунку прогнозу проілюструємо для випадку найпростішої -моделі в стандартному вигляді:
. (5.2.13)
Перепишемо (5.2.13) в матричному вигляді:
. (5.2.14)
Для спрощення виключимо з (5.2.14) вектор і отримаємо
. (5.2.15)
Таким чином, якщо дійсні значення за (1)-моделлю (5.2.15) в період часу (): , то відповідно прогнозні значення в період часу ():
, оскільки .
Вектор помилок прогнозу в період часу () дорівнює .
Вектор дійсних значень за (l)-мoдeллю в період часу ()
.
Прогнозні значення Y в період ()
.
Помилки прогнозу
.
Відповідно для періоду () отримаємо:
. (5.2.16)
. (5.2.17)
Помилки прогнозу
. (5.2.18)
Якщо позначити VAR-COV-матрицю векторів випадкових величин через , то з виразу (5.2.18) легко побачити, що VAR-COV-матриця для помилок в період () відповідно дорівнює:
. (5.2.19)
Ілюстрація принципу прогнозування на основі найпростішої VAR-моделі демонструє надзвичайну простоту отримання прогнозів, коли вся необхідна для цього інформація міститься лише в часових рядах досліджуваних змінних. При цьому модель уникає довільних обмежень економічної теорії і, разом із тим, шляхом включення декількох змінних можна подолати обмеженість одновимірних моделей. Сучасні пакети прикладних програм дозволяють отримати прогнози для VAR-моделей вищих порядків з великою кількістю досліджуваних показників.
Імпульсний аналіз. На відміну від ARIMA- VAR-моделі дозволяють проводити економічний аналіз результатів. Звичайно, самі коефіцієнти VAR-моделей важко тлумачити, але можна дати інтерпретацію результатів функції імпульсних відгуків (impulse responsible function) та декомпозиції дисперсій (variance decomposition) [30].
Розглянемо стандартну – модель (5.2.9). Елемент кожної матриці коефіцієнтів показує, як зміниться значення в залежності від j -го шоку періодів назад. Таким чином
= . (5.2.20)
Вираз як функція від називається функцією імпульсних відгуків. Вона показує зміну ендогенних показників у відповідь на шок (зміну одного зі збурень системи). За допомогою цієї функції можна досліджувати, який вплив на майбутні значення мають відповідні шоки в минулому.
Приклад 5.2.1. Проілюструємо ідею імпульсного аналізу простим прикладом. Для -моделі (5.2.13), або у матричному вигляді: , для спрощення припускаємо, що вектор (перетини) відсутній, тобто в матричному вигляді маємо: .
Нехай нам відома матриця коефіцієнтів: та варіаційно-коваріаційна матриця збурень: VAR-COV = . Перший елемент варіаційно-коваріаційної матриці є дисперсією першого збурення, тобто =9. Побудуємо імпульсну функцію в припущенні, що перше збурення змінюється на одне середньоквадратичне відхилення, тобто на 3. Крім того, припустимо, що початкові значення ендогенних змінних дорівнюють нулю:
; .
За нашим припущенням, в перший період часу зростає на 4, а в інші проміжки часу знову спадає до нуля; друге збурення залишається без змін. Проаналізуємо ланцюгову зміну Y як реакцію на одноразовий шок, викликаний зміною першого збурення.
+=.
+=.
+=.
+=…………… .
Цей процес можна продовжити далі, відповідно імпульсна функція має вигляд:
| Імпульсна функція (IRF) | ||
| від = (30) | ||
| Період | ||
| 1 | 3 | 0 |
| 2 | 0.9 | 1.5 |
| 3 | 0.42 | 0.85 |
| 4
… |
0.211
… |
0.38
… |
Сучасні пакети видають графічне зображення імпульсної функції. Л логічно можна побудувати імпульсну функцію для другого збурення. Отже, вона вимірює ефект на значення ендогенних змінних системи в поточний та майбутні періоди часу, викликаний зміною одного з показників у поточний період часу на одне середньоквадратичне відхилення в поточний період часу.
Зауважимо, що у VAR-моделях в приведеній формі інтерпретація імпульсної функції ускладнюється, оскільки збурення в такій системі, на відміну від структурної форми, корелюють між собою. Якщо кореляція існує, то відповідно є загальний компонент, який не може бути пов’язаний лише з однією змінною. Вирішенням цієї проблеми є представлення збурень приведеної форми VAR-моделі через збурення структурної форми, які за припущенням не корелюють між собою.
Приклад 5.2.2. Розглянемо приклад застосування VAR-моделі залежності між щоквартальним споживанням та доходом, що залишається у розпорядженні домогосподарств, для прогнозування змін цих показників у майбутньому. Для розрахунку використана VAR(15)-модель, побудована в [28].
Введемо наступні позначення:
LNC – ряд логарифмів реальних значень споживання короткострокових товарів (квартальна інформація);
DLNC – ряд перших різниць логарифмів реальних значень споживання короткострокових товарів (квартальна інформація);
LNY – ряд логарифмів реальних значень доходу, що залишається у розпорядженні домогосподарств (квартальна інформація);
DLNY – ряд перших різниць логарифмів реальних значень доходу, що залишається у розпорядженні домогосподарств (квартальна інформація). Дані наведені в таблиці додатку 2.
В умовах нашого прикладу прогнозна модель має вигляд:
DLNC = 0,180747*dlnc(-l) + 0,15785*dlnc(-2) + 0,186318*dlnc(-3) – 0,118597*dlnc(-4) –
-0,159071 *dlnc(-5) + 0,044545*dlnc(-6) + + 0,057238*dlnc(-7) – 0,18603*dlnc(-8) –
-0,027484*dlnc(-9) – 0,064276*dlnc(-10) + 0,074662*dlnc(-ll) – 0,023077*dlnc(-12) –
-0,2210412*dlnc(-13) +0,067216*dlnc(-14) + 0,080324*dlnc(-15) + 0,1002762*dlny(-l) –
-0,0226551*dlny(-2) – 0,02245*dlny(-3) + + 0,04362*dlny(-4) – 0,038752*dlny(-5) + +0,10493*dlny(-6) + 0,02203*dlny(-7) – 0,0219819*dlny(-8) + 0,08115*dlny(-9) +
+0,087531*dlny(-10) + 0,033678*dlny(-ll) – 0,00359*dlny(-12) – 0,003627*dlny(-13) +
+0,01379017*dlny(-14) – 0,02935*dlny(-15) + 0,004737;
DLNY = 0,6766198*dlnc(-l) + 0,10746*dlnc(-2) + 0,39290*dlnc(-3) + 0,428478*dlnc(-4) –
-0,04092*dlnc(-5) + 0,149560*dlnc(-6) + 0,04093*dlnc(-7) – 0,09684*dlnc(-8) +
+0,04015279*dlnc(-9) – 0,01189*dlnc(-10) + 0,0865279*dlnc(-ll) + 0,336836*dlnc(-12) –
-0,18805*dlnc(-13) – 0,149673*dlnc(-14) – 0,18498*dlnc(-15) – 0,178798*dlny(-l) –
-0,093591*dlny(-2) – 0.128621*dlny(- 3) – 0,143853*dlny(-4) – 0,228075*dlny(-5) +
+0,0714324*dlny(-6) – 0,099384*dlny(-7) – 0,1367433*dlny(-8) + 0,0514864*dlny(-9) +
+0,114193*dlny(-10) + 0,021236*dlny(-ll) – 0,079146*dlny(-12) –0,013706*dlny(-13) +
+0,02128*dlny(-14) + 0,079392*dlny(-15) + 0,0016.
Таблиця 5.2.1
Результати оцінки моделі
| DLNC | DLNY | |
| С | 0.004738
(0.00144) [ 3.29229] |
0.001628
(0.00251) [ 0.64787] |
| R-squared | 0.323273 | 0.330931 |
| Adj. R-squared | 0.196387 | 0.205481 |
| Sum sq. resids | 0.003505 | 0.010684 |
| S.E. equation | 0.004680 | 0.008172 |
| F-statistic | 2.547743 | 2.637944 |
| Log likelihood | 770.4932 | 664.0507 |
| Akaike AIC | -7.743384 | -6.628803 |
| Schwarz SC | -7.215528 | -6.100947 |
| Mean dependent | 0.007989 | 0.008099 |
| S.D. dependent | 0.005221 | 0.009168 |
Імпульсний аналіз на основі оціненої VAR-моделі. Аналіз оцінених коефіцієнтів у VAR-моделях, особливо для виявлення короткострокових ефектів, часто не має великого значення, оскільки дуже важко відокремити частковий миттєвий ефект від зміни певної змінної, особливо коли кількість лагів є значною. Ось чому для кращого розуміння динамічних властивостей моделі кориснішим є аналіз імпульсних функцій відгуків (impulse response functions — IRF). Його можна зробити, вибравши Impulse у вікні VAR-об’єкта. При цьому потрібно задати прогнозний горизонт (Periods); змінні, які впливають на досліджувані значення (‘affecting’ variables) (Innovations to:), та змінні, що піддаються впливу (‘affected’ variables» (Cause Responses by:). Варто зауважити, що число періодів треба обирати достатньо великим, щоб можливо було побачити, чи є система стабільною. Імпульсна функція відгуків (IRF) показує явну динаміку зміни всіх змінних всередині системи у відповідь на зміну на одне середньоквадратичне відхилення однієї з них. Для нашого прикладу функції імпульсних відгуків представлено на рис. 5.2.1.
Response of DLNC to One S.D. Innovations Response of DLNY to One S.D. Innovations
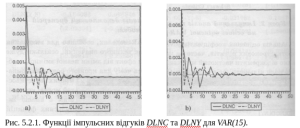
Рис. 5.2.1. Функції імпульсних відгуків DLNC та DLNY для VAR(15).
Рисунок 5.2.1.а) показує, як зміни на одне середньоквадратичне відхилення (шок одного стандартного відхилення) в DLNY (пунктирна лінія) та в DLNC (суцільна лінія) впливають на зміну натурального логарифма споживання (DLNC). З зовнішнього вигляду імпульсних функцій відгуків можна помітити, наприклад, що зміна DLNY (зміна в доході) в одне середньоквадратичне відхилення викликає спочатку позитивні зміни у споживанні, але згодом матиме негативні наслідки. Тому чистий ефект від змін у доході не є ясним. Загалом це відповідає теорії постійного доходу, коли споживання слабко залежить від поточного доходу. Тим не менше не важко помітити, що флуктуації зменшуються і наближаються до нуля зі зростанням часу. З іншого боку, шок в DLNC справляє відносно сильний і тривалий позитивний ефект на динаміку DLNC, що також відповідає теорії постійного доходу. В підсумку, система є стабільною, оскільки відгук згасає та асимптотично наближається до нуля, і система врешті-решт досягає певного стійкого стану. Рисунок 5.2.1.b) показує відповідь DLNY на шоки в DLNY (пунктирна лінія) та в DLNC (суцільна лінія).
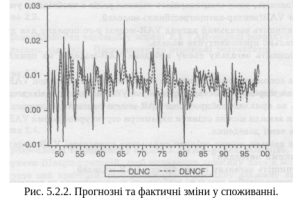
Рис. 5.2.2. Прогнозні та фактичні зміни у споживанні.
Прогноз на основі оціненої VAR-моделі. Оцінену VAR(15)-модель використаємо для прогнозування змін у доході та споживанні. Для отримання прогнозу необхідно надати явні значення екзогенним змінним для періоду прогнозування. В даному випадку наша модель має тільки ендогенні змінні, тому їх значення задавати не потрібно. Результати прогнозу, на основі оціненої VAR(15)-моделі показані на рисунках 5.2.2 та 5.2.3.

Рис. 5.2.3. Прогнозні та фактичні зміни у доході.
Як можна побачити з наведених графіків, прогнозна значення обох змінних, обчислені за VAR(15)-моделлю, досить точно відображають фактичні значення. Отже, прогнозування на основі VAR-моделей є достатньо ефективною процедурою.
5.3. Прогнозування на основі моделей коригування помилки (коінтегрування). Основним припущенням моделювання та прогнозування за -моделями є стаціонарність часових рядів. Наявність стаціонарності також важлива при вивченні співвідношень між різними рядами. При обговоренні нестаціонарних рядів у параграфі 1.2. було введено поняття інтегрованих рядів, які перетворюються на стаціонарні шляхом переходу до різниць. Проте, внаслідок такого перетворення втрачаються зв’язки між динамічними рядами і важлива довгострокова інформація. Одним з можливих шляхів розв’язання цієї проблеми при моделюванні на основі часових рядів є застосування моделі коригування помилки (ЕСМ). Головною ідеєю цього підходу є оцінка довгострокового рівноважного взаємозв’язку (на основі значень відповідних часових рядів у рівнях) між досліджуваними показниками та його комбінація з короткостроковими зв’язками (оціненими на основі перетворених часових рядів у різницях). Побудова моделі коригування помилки є коректною тільки у випадку коінтегрування часових рядів.
Коінтегрування часових рядів. Спочатку суть коінтеграції проілюструємо на прикладі. Припустимо, що два ряди та є обидва , тоді, взагалі кажучи, будь-яка їх лінійна комбінація також буде . Простим прикладом є споживання () та дохід (), пов’язані між собою рівнянням регресії . За довгий проміжок часу дані про ці змінні свідчать про наявність сильно зростаючих трендів, і їх різниця (заощадження) також має зростаючий тренд. Однак іноді буває, що комбінація двох -рядів є насправді -рядом. Так, лінійна функція споживання, що складається з -змінних, може мати стаціонарні залишки, тобто споживання та прибуток є коінтегрованими. Більш формально, якщо нова змінна може бути визначена як
, (5.3.1)
де и є , тоді кажуть, що та коінтегровані, а називається сталою коінтегрування або, у випадку більш ніж двох змінних, множина значень є вектором коінтегрування. Змінну и можна інтерпретувати як похибку і за допомогою сталої, що її можна включити до (5.3.1), можна зробити рівним нулю середнє значення похибки, тобто перетворити у коінтегративне регресійне рівняння. Це пов’язано з коінтегративною регресійною статистикою Дурбіна-Уотсона з параграфа 1.3, до якої ми повернемося нижче.
Більш загальне поняття коінтеграції є таким. Нехай часові ряди та є інтегрованими порядку d, тобто І(d). Тоді, як правило, лінійна комбінація цих двох рядів також буде І(d). Але якщо, існує лінійна комбінація цих рядів І(d-b), тоді ці ряди називаються коінтегрованими порядку (d,b), що позначають . Якщо відповідна лінійна комбінація може бути записана у формі , де , то вектор називається коінтеграційним вектором. У попередньому прикладі змінні та є , тому d=b=1, та коінтеграційний вектор .
Зазначимо наступні властивості коінтегрованих змінних:
- включення сталої в (5.3.1) не дає ніякого ефекту;
- доведено, що коінтегрованість змінних означає коінтегрованість їх логарифмів, тоді як коінтегрованість логарифмів змінних не означає коінтегрованості самих змінних (звідси випливає, що для вибору конкретної функціональної форми бажано провести деякі дослідження нелінійних перетворень змінних у коінтегративних співвідношеннях);
- коінтегрування передбачає, що дві змінні не рухаються окремо, оскільки и, що є мірою розходження між та , може бути розглянута як “похибка”, є стаціонарною з нульовим середнім. Це твердження можна записати у вигляді
(5.3.2)
і тлумачити як обмежене або рівноважне співвідношення між х та у. Динамічний шлях коінтегрованих рядів можна уявити (рис. 5.3.1) як поточне відхилення від довгострокової рівноваги.
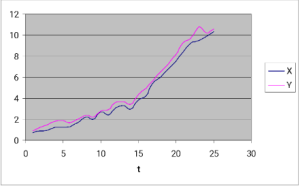
Рис.5.3.1. Коінтеграція двох часових рядів
4) доведено, що коли та обидва є , мають сталі середні значення та є коінтегрованими, тоді існує механізм генерації даних з “корекцією похибки” або модель корекції похибки (ЕСМ).
Модель корекції похибки (ЕСМ). Лінійна комбінація змінних є лише оцінкою довгострокового зв’язку і не відображає короткострокової динаміки. Для того, щоб поглибити економетричний аналіз та поліпшити точність моделювання, Інгл та Гренджер запропонували розглядати модель коригування помилки, яка об’єднувала б довгостроковий зв’язок для досліджуваних змінних з лагом одиниця та короткострокову динаміку, виражену залежністю різниць ендогенних змінних від поточних та лагових (затриманих на деякий проміжок часу) різниць екзогенних змінних. Найпростіша модель коригування помилки для випадку двох змінних та має такий формалізований вигляд:
, (5.3.3)
, (5.3.4)
де и задається (5.3.1), d(L) є поліномом скінченного порядку від лаг-оператора L та похибки та є сумісними процесами білого шуму, які є, можливо, корельованими при однакових значеннях t і .
Остання умова означає, що и зустрічається принаймні у одному з рівнянь. Справедливість (5.3.3) та (5.3.4) випливає з того, що та є , отже, їх різниця є і тому кожен доданок є .
Моделі корекції похибкі широко використовуються в економіці. Вони вимагають наявності добре визначеної рівноваги економічної системи і щоб швидкість руху змінних у напрямку положення рівноваги відображала відстань системи до положення рівноваги. Отже, коінтегративне рівняння (5.3.1) відображає положення рівноваги даної системи. Абсолютне значення величини вимірює відстань до положення рівноваги у попередній момент часу. Механізм корекції похибки може з’явитися у моделях фінансових ринків за умови, коли очікувані суб’єктами майбутні значення змінних втілені у поточній змінній. Зазначимо, що не тільки коінтегровані змінні повинні задовольняти такій моделі, але вірне і обернене: дані, породжені ЕСМ, також повинні бути коінтегрованими.
Цей результат має велике значення, оскільки пов’язує дві раніше окремі області: моделі часових рядів та ЕСМ. Якщо кілька змінних є коінтегрованими, то існує їх векторне ARMA-зображення. У стандартній VARMA -моделі нема обмежень щодо взаємного руху декількох часових рядів. Саме коінтеграція дозволяє досліднику вводити до відповідної системи необхідний зв’язок між змінними, що призводить до більш точного оцінювання моделі.
Побудова та коректне застосування моделей коригування помилки з метою прогнозування передбачає послідовне виконання наступних етапів:
- перевірка рядів на стаціонарність;
- визначення порядку інтеграції кожного ряду;
- тестування рядів на коінтеграцію;
- оцінювання моделі та перевірка на адекватність.
Критерії визначення порядку інтегрованості та коінтегрованості рядів. У параграфі 1.3 ми бачили, як коінтегративний регресійний критерій Дарбіна-Уотсона (КРДУ) (1.3.14) та критерій Дікі-Фуллера (1.3.16) можна використати для перевірки порядку інтегрованості одного ряду. Тепер розглянемо їх більш загальне використання. Спочатку перепишемо критерій перевірки, чи є два ряди коінтегрованими (5.3.1), у вигляді
. (5.3.5)
Оцінки параметрів рівняння знаходяться за допомогою звичайного метода найменших квадратів і обчислюєтся статистика Дарбіна-Уотсона. Аналіз (1.3.14) показав, що коли КРДВ перевищує критичне значення, то и є і та є коінтегрованими. Можна очікувати, що для коінтегрованих змінних значення R2 буде досить великим.
Критерій Дікі та Фуллера розглядає залишки з (5.3.5) для оцінки
(5.3.6)
і потім перевіряє, чи є значимо від’ємним. Для цього використовуються таблиці Дікі та Фуллера, і якщо є значущим, то и є , отже, та є коінтегрованими. Коли залишки у (5.3.6) не є білим шумом, рівняння можна модифікувати включенням сталої і додаткових значень за минулі періоди, поки залишки не стануть білим шумом (за розширеним тестом Дікі—Фуллера [ADF]). Якщо похибки є стаціонарними, то можна зробити висновок, що оцінена лінійна комбінація досліджуваних змінних насправді є рівнянням коінтеграції, тобто що змінні коінтегрують. Якщо дорівнює нулю, то кажуть, що и має одиничний корінь.
Якщо встановлено, що дві (або більше) змінні є коінтегрованими, можна вибрати модель корекції похибки та оцінити її параметри. Енгл та Гренджер запропонували двохетапну процедуру, у якій на першому етапі для одержання оцінок залишків за допомогою метода найменших квадратів знаходяться оцінки параметрів регресії (5.3.5). При наявності більш ніж двох коінтегрованих змінних важливо перевірити, чи всі вони необхідні. Друга стадія процедури полягає у підстановці оцінок залишків з (5.3.5) замість у загальну модель корекції похибки (5.3.3) та (5.3.4) і оцінюванні параметрів цих рівнянь.
Якщо критерії свідчать, що змінні не с коінтегрованими, це означає некоректність теоретичної моделі, зокрема, можливо, що випущено важливі змінні. Для досягнення коінтегровності можна додавати нові змінні. Однак, знаходження коінтегрованих змінних повинно бути сигналом для початку перевірки коінтегрованості підмножин цих змінних.
Приклад 5.3.1. Для ілюстрації побудови моделі коригування похибки (ЕСМ) розглянемо прогнозування надходження податку на додану вартість (ПДВ) до Зведеного бюджету України [28].
Введемо такі позначення:
ПДВ – податок на додану вартість у номінальному вимірюванні (млрд грн);
ICЦ – індекс споживчих цін;
ПДВР – податок на додану вартість у реальному вимірюванні (ПДВР = ПДВ/ІСЦ);
ПДВРС – податок на додану вартість, очищений від сезонності;
ВВП – валовий внутрішній продукт у номінальному вимірюванні (млрд грн);
ВВПР – валовий внутрішній продукт у реальному вимірюванні (ВВПР = ВВП/ІСЦ);
ВВПРС – валовий внутрішній продукт, очищений від сезонності.
Для побудови моделі коригування похибки для двох змінних: ПДВ та ВВП були використані реальні щомісячні дані.
Виконання завдання передбачає декілька кроків.
Крок 1. Перевірка виконання передумов коінтеграції. Перед побудовою моделі коригування похибки спершу необхідно перевірити, чи є розглядувані часові ряди нестаціонарними однакового порядку. Якщо так, можна перейти до кроку 2. Якщо ні, то неможливо побудувати модель коригування похибки. За допомогою розширеного тесту Дікі-Фуллера можна показати, що реальні надходження ПДВР є нестаціонарним рядом, порядок інтеграції якого дорівнює одиниці, реальні податкові надходження, скориговані на сезонність (ПДВРС), та реальний ВВПР, скорегований на сезонність (ВВПРС), є також нестаціонарними часовими рядами з порядком інтеграції один (І(1)). Попередній аналіз часових рядів ПДВ та ВВП (у реальному вимірюванні та очищених від сезонності) показав, що вони є нестаціонарними однакового порядку інтеграції. Отже, передумови для коінтеграції виконано. Тепер ряди потрібно перевірити на наявність коінтеграції.
Крок 2. Перевірка часових рядів на коінтеграцію за методикою Інгла–Гренджера. Щоб перевірити часові ряди на коінтеграцію, маємо спочатку оцінити довготривалу залежність між надходженнями від ПДВ (ПДВРС) та ВВП (ВВПРС) звичайним методом найменших квадратів (використовують реальні та сезонно скориговані змінні), а потім перевірити похибки оціненої моделі на стаціонарність.
Оцінене регресійне рівняння залежності між надходженнями від ПДВ (ПДВРС) та ВВП (ВВПРС) методом найменших квадратів статистично значуще на рівні 0,05 і має вигляд: ПДВРС = -0,002 + 0,126×ВВПРС. Як можна побачити, зростання на 1 млрд грн реального ВВП приводить до зростання надходжень ПДВ приблизно на 126 млн грн.
Щоб дійти висновку стосовно коінтеграції часових рядів, необхідно перевірити на стаціонарність похибки, розраховані на підставі оціненого вище рівняння. Використовують тест Дікі-Фуллера (ADF). Слід пам’ятати, що йдеться про справдження гіпотези щодо а=0 в такому рівнянні: . Тобто перевіряється гіпотеза про наявність одиничного кореня. Якщо нульова гіпотеза відхиляється, можна зробити висновок про стаціонарність похибок, або, інакше, про існування коінтеграції (довгострокової залежності) між змінними. Таким чином, можна переходити до наступного кроку, тобто до побудови моделі коригування похибки.
Крок 3. Побудова моделі коригування похибки за методикою Інгла–Гренджера.
Оскільки виявлена наявність коінтеграції між ПДВ та ВВП, можна оцінити модель коригування похибки для цих змінних, тобто побудувати залежність перших різниць реальних очищених від сезонності значень ПДВ (ПДВРС) від перших різниць реальних очищених від сезонності значень ВВП (ВВПРС) та відхилення від довготривалої рівноваги із одиничним лагом. Зазначимо, що в модель включені фіктивні змінні для 1997 фіскального року, для грудня 1997 і січня 1998 р. (фіктивні змінні дорівнюють одиниці для всіх місяців 1997 р. та нулю для решти місяців). Модель коригування похибки має вигляд:
∆ПДВРСt = −0.4508×(ПДВРСt-1 − 0.1023×ВВПРСt-1 + 0.001225) +
+ 0.0465×∆ПДВРСt-1 − 0.5691×∆ПДВРСt-2 − 0.0978×∆ВВПРСt-1 +
+ 0.0674×∆ВВПРСt-2 + 0.00134×DUMMY9712 − 0.0011×DUMMY9801 +
+ 0.000316×DUMMY97
∆ВВПРСt = −1.635×(ПДВРСt-1 − 0.1023×ВВПРСt-1 + 0.00125) −
− 0.0627×∆ПДВРСt-1 − 1.2064×∆ПДВРСt-2 − 0.5681×∆ВВПРСt-1 −
− 0.1444×∆ВВПРСt-2 + 0.0028×DUMMY9712 + 0.000129×DUMMY9801 +
+ 0.0010×DUMMY97.
Використовуючи ці результати, можна визначити довгострокову залежність між змінними (коефіцієнти нормалізовані таким чином, щоб коефіцієнти, які стоять при залежних змінних, дорівнювали одиниці). Прокоментуємо отримані результати й звернемо увагу на окремі моменти.
- Система стабільна відносно змінної ПДВРС (коефіцієнт відхилення від довготривалої рівноваги (коінтеграційне рівняння) дорівнює −0.45), але нестабільна з точки зору іншої змінної − ВВПРС (−1.63). Утім потрібно зазначити, що ВВПРС є слабко екзогенною, оскільки оцінений коефіцієнт є статистично незначущим за відносно низького рівня довіри.
- Кількість лагів у прикладних дослідженнях часто обирають, виходячи з максимальних значень Акайк- та Шварц-критеріїв, якщо немає попередньої апріорної інформації щодо прийнятної кількості.
Крок 4. Прогнозування на основі оцінюваної моделі коригування похибки. Раз оцінивши модель, можемо використати її для прогнозування податкових надходжень. Щоб зробити прогноз, розв’язують модель, надаючи конкретні значення екзогенним змінним у прогнозовому горизонті. У цьму разі модель складається лише з одного рівняння, тому має дуже простий вигляд:
∆ПДВРСt = −0.4508×(ПДВРСt-1 − 0.1023×ВВПРСt-1 + 0.001225) +
+ 0.0465×∆ПДВРСt-1 − 0.5691×∆ПДВРСt-2 − 0.0978×∆ВВПРСt-1 +
+ 0.0674×∆ВВПРСt-2 + 0.00134×DUMMY9712 − 0.0011×DUMMY9801 +
+ 0.000316×DUMMY97
Звичайна найпростіша перевірка якості прогнозу полягає у візуальному порівнянні фактичних і теоретично обчислених значень часових рядів. На рис. 5.3.1 відображено фактичні та прогнозові значення ПДВ (у реальному вимірі та очищеному від сезонності).
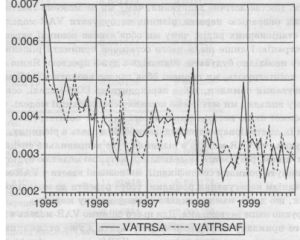
Рис. 5.3.1. Фактичні (−−) та прогнозові (—) значення ПДВ (в реальному вимірі та очищеному від сезонності)
Візуальний аналіз демонструє, що прогнозові значення (теоретично розрахований ряд) досить непогано «відображають» фактичні. Звичайно, висновки, зроблені на підставі візуального аналізу, слід підкріпити формальними критеріями якості прогнозу
При застосуванні коінтеграційного методу існують три труднощі, на які варто звернути увагу. Перша має статистичну природу і полягає у тому, що потужність критеріїв перевірки гіпотези про рівність кореня до одиниці у випадку, коли справжнє значення близьке до одиниці, часто дуже низька, якщо кількість спостережень невелика. У таких ситуаціях гіпотеза про рівність кореня до одиниці приймається, коли справжнє значення є, скажімо, 0,96. Однак у цьому випадку подальшу інформацію відносно того, чи є ряд коінтегрованим, чи ні, можна одержати шляхом перевірки значущості коефіцієнтів при у рівняннях корекції похибки. Друга проблема стосується вибору залежної та незалежної змінної у коінтеграційній регресії. Якщо та – дві коінтегровані змінні, то та є однаково вірні зображення, тобто використання або або як залежної змінної, у випадку двох змінних, дасть однакові оцінки для при великому значенні R2. Енгл та Гренджер показали, що цей результат, як правило, має місце на практиці. У загальному випадку, якщо у коінтегративній регресії є k змінних, коінтегративний вектор не буде єдиним. Це породжує проблеми у інтерпретації моделей корекції похибки. Третя проблема полягає у тому що, хоча, співвідношення рівноваги у структурній моделі, скоріше за все, не змінюватимуться у відповідь на зміну економічної політики, це, взагалі, не буде вірним відносно пристосування до положення рівноваги. Тому модель корекції похибки буде змінюватися разом з економічною політикою. Однак треба мати на увазі ті ж самі міркування відносно ймовірностей зміни політики, які було зроблено для ARMA-моделей. Додамо також, що припущення про те, чи параметри с сталими на протязі всього періоду, що вказує на стабільність співвідношень, які лежать в основі моделі, можна легко перевірити звичайним методом переоцінення на під-періодах.