Задача згладжування часового ряду має наступне формулювання. Для реалізації (часового ряду) () деякого випадкового процесу потрібно найкращим чином визначити оцінку деякої невипадкової компоненти (тренду) , яка в кожний фіксований момент часу є середнім значенням випадкової величини і відображає основні закономірності зміни досліджуваного показника у часі.
3.1. Прогнозування тенденції часового ряду за середніми характеристиками.
Найпростішим способом прогнозування вважається підхід, який визначає прогнозну оцінку від фактично досягнутого рівня за допомогою середнього рівня, середнього приросту, середнього темпу зростання.
Екстраполяція на основі середнього рівня ряду. При екстраполяції соціально-економічних процесів на основі середнього рівня ряду прогнозоване значення береться як середнє арифметичне значення минулих рівнів ряду, тобто точковий прогноз , зроблений в момент часу на період упередження , розраховується за формулою:
. (3.1.1)
Інтервал надійності для прогнозу середньої при невеликій кількості спостережень визначається як
, (3.1.2)
де – критичне значення – критерію Стьюдента із ступенями вільності і рівнем значущості ; – середня квадратична похибка середнього (, де s – середньоквадратичне відхилення спостережень).
Одержаний інтервал надійності враховує невизначеність, яка криється в оцінці середньої величини. Однак залишається припущення, що прогнозований показник дорівнює середньому вибірковому значенню, тобто при такому підході не враховується те, що окремі значення показника коливалися навкруги середнього в минулому і це також буде відбуватися в майбутньому. Отже загальна дисперсія включає коливання вибіркової середньої й коливання індивідуальних значень навкруги середнього і складає величину , а інтервал надійності для прогнозованої оцінки ряду дорівнює:
, (3.1.3)
Екстраполяція за середнім абсолютним приростом може бути виконана у тому разі, коли загальна тенденція розвитку вважається лінійною. Прогнозна оцінка одержується за формулою:
, (3.1.4)
де – середній абсолютний приріст.
Екстраполяція за середнім темпом зростання виконується у випадку, коли є підстава вважати, що загальна тенденція динамічного ряду характеризується експоненціальною кривою. Прогноз , зроблений в момент часу на період упередження , у цьому випадку розраховується за формулою:
, (3.1.5)
де – середній темп зростання, розрахований за середньою геометричною.
Інтервал надійності прогнозу за середнім абсолютним приростом і середнім темпом зростання можна одержати тільки тоді, коли ці середні визначаються за допомогою статистичного оцінювання параметрів відповідно лінійної та експоненціальної кривої (див. 3.2).
Усі три способи привертають увагу багатьох працівників статистичних органів завдяки своїй простоті та легкості реалізації. Однак, крім вказаних позитивних якостей, вони мають декілька суттєвих недоліків. По-перше, всі фактичні спостереження є результатом закономірності та випадковості, отже виходити тільки з останнього спостереження неправильно. По-друге, немає можливості оцінити слушність використання середньої характеристики ряду в кожному конкретному випадку. По-третє, не завжди можна розрахувати інтервал надійності, в середину якого потрапляє прогнозована величина, і визначити його імовірність. У зв’язку із цим екстраполяція за середніми характеристиками ряду застосовується лише як орієнтир майбутнього розвитку або якщо неможливо використати інші статистичні методи (наприклад, при дуже малій кількості спостережень).
3.2. Прогнозування тенденції часового ряду за аналітичними методами згладжування.
До методів аналітичного згладжування відносять регресійний аналіз разом із методом найменших квадратів та його модифікаціями. Виявити основну тенденцію аналітичним методом – означає надати досліджуваному процесу однаковий розвиток на протязі усього часу спостереження. Тому для цих методів важливо вибрати оптимальну функцію детермінованого тренду (кривої зростання), яка згладжує ряд спостережень .
Регресійний аналіз. Оцінювання параметрів кривих зростання робиться на основі побудови моделі регресії, в якій пояснюючою змінною є час
(3.2.1)
де – функція тренду (крива зростання);
– невідомі випадкові похибки.
Виходячи із теоретичних міркувань крива зростання може описуватися будь-якою математичною функцією . Оцінка цієї функціональної залежності здійснюється за вибірковими спостереженнями {t,}, , а вибір методу оцінювання залежить від виду кривої і стохастичного походження випадкових похибок . Якщо функція лінійна за параметрами, наприклад, має вид алгебраїчного поліному ступеня p:
, (3.2.2)
і при цьому довжина часового ряду суттєво перевищує ступінь поліному , а випадкові залишки мають властивості “білого шуму”, тобто
, (3.2.3)
то оцінки параметрів можна одержати методом найменших квадратів (МНК). МНК-оцінки параметрів лінійної регресії за умови мінімізації суми квадратів відхилень точок вхідного часового ряду від їх згладжених значень : (3.2.4)
розраховуються за формулою:
, (3.2.5)
де – матриця значень спостережень пояснюючих змінних розмірністю , яка у випадку (3.2.2) має вигляд
, а вектор-стовпець спостережень залежної змінної .
Побудована модель прогнозу повинна супроводжуватися додатковою інформацією про її точність та адекватність. Якщо умова сталості дисперсії і взаємної незалежності випадкових похибок моделі (3.2.3) не виконується, то застосовують узагальнений МНК; модель, в якій функція є нелінійною за параметрами, потребує техніки статистичного аналізу нелінійних моделей регресії тощо.
Для розрахунку в момент часу прогнозної оцінки на період упередження , потрібно оцінити параметри лінійного тренду і підставити їх у рівняння тренду (наприклад, (3.2.2)), де .
Методи, що розроблені для статистичних сукупностей, дозволяють визначити інтервал надійності прогнозу, який залежить від стандартної похибки оцінки прогнозованого показника, від часу упередження прогнозу, від довжини прогнозної бази та від обраного рівня значущості.
Наприклад, у випадку прямолінійного тренду інтервал надійності прогнозу має вигляд
, (3.2.6)
де – період упередження;
– точковий прогноз на момент часу ;
п – кількість спостережень у часовому ряду (довжина прогнозної бази);
– стандартна похибка (середньоквадратичне відхилення) оцінки , =;
– табличне значення критерію Стьюдента для рівня значущості α і числа ступенів волі .
Іноді для розрахунку інтервалів надійності прогнозу відносно лінійного тренду застосовують наведену вище формулу у дещо перетвореному вигляді:
, або , (3.2.7)
якщо перенести початок відліку часу на середину періоду спостережень (= 0), де t – порядковий номер рівня ряду (t = 1, 2,…,п); – час, для якого робиться прогноз; – час, що відповідає середині періоду спостережень вхідного ряду; підсумок робиться за усіма спостереженнями.
Формула для розрахунку інтервалів надійності прогнозу відносно тренду, який має вид поліному другого або третього порядку, виглядає наступним чином:
. (3.2.8)
Аналогічно розраховуються інтервали надійності для кривих зростання, які можна звести до лінійної функції.
Розглянутий розрахунок інтервалів надійності прогнозів на основі кривих зростання, що спирається на висновки і формули теорії регресійного аналізу, для часових рядів не зовсім правомірний, оскільки динамічні ряди, як вже відмічалось, відрізняються від статистичних сукупностей. Тому до оцінювання інтервалів надійності для кривих зростання слід підходити з певною обережністю. Якщо припустити, що випадкова змінна () є стаціонарним часовим рядом, то похибка прогнозу становитиме
. (3.2.9)
Звідси
. (3.2.10)
Динамічним мультиплікатором збурення , тобто величиною, яка показує, на скільки зміниться значення часового ряду через періодів в залежності від поточного збурення, є . Очевидно, що вплив збурення буде спадати з часом, тому .
Методи прогнозування, основані на методах регресії, використовуються для короткострокового та середньострокового прогнозування. Вони не допускають адаптації: з отриманням нових даних процедура побудови прогнозу повинна бути повторена спочатку. Оптимальна довжина періоду упередження визначається окремо для кожного економічного процесу з врахуванням його статистичної нестабільності. Ця довжина, як правило, не перевищує для рядів річних спостережень однієї третини обсягу даних, а для квартальних і місячних рядів – двох років.
Види кривих зростання. Для відображення економічних процесів існує велика кількість видів кривих зростання. Щоб правильно підібрати найкращу криву для моделювання і прогнозування економічного явища, необхідно знати особливості кожного виду кривих. Криві зростання описують різні тенденції економічних процесів, наприклад, життєвий цикл товару, процес нагромадження капіталу, маркетингові зусилля фірм тощо. Економічна практика вже надбала певний досвід і певні типи кривих, які найчастіше використовуються в соціально-економічних дослідженнях. До таких кривих належать: поліноміальні, експоненціальні і S-подібні криві зростання.
Поліноміальні криві зростання можна використовувати для апроксимації (наближення) і прогнозування економічних процесів, у яких майбутній розвиток не залежить від досягнутого рівня. Простіші поліноміальні криві зростання мають вид:
(поліном першого ступеня),
(поліном другого ступеня), (3.2.11)
(поліном третього ступеня) тощо
Поліноміальні моделі лінійні за параметрами. Параметри цих моделей (лінійної, квадратичної, поліному третього ступеня) мають такі економічні тлумачення: а1 – лінійний приріст, а2 – прискорення зростання, а3 – характеризує динаміку прискорення зростання.
Для поліному першого ступеня характерний постійний приріст. Якщо розрахувати перші прирости за формулою , t = 2, 3, …, n, то вони будуть постійними величинами і дорівнюватимуть а1.
Якщо перші прирости розрахувати для поліному другого ступеня, то вони будуть мати лінійну залежність від часу і ряд із перших приростів на графіку буде представлений прямою лінією. Другі прирости для поліному другого ступеня будуть постійними.
Для поліному третього ступеня перші прирости будуть поліномами другого ступеня, другі прирости будуть лінійною функцією часу, а треті прирости, що розраховуються за формулою , будуть постійними величинами.
Звідси можна відзначити наступні властивості поліноміальних кривих зростання:
- від поліному високого ступеня можна шляхом розрахунку послідовних різниць (приростів) перейти до поліному нижчого порядку;
- значення приростів для поліномів будь-якого порядку є сталими величинами.
Експоненціальні криві використовуються для зображення швидко зростаючих або спадаючих економічних процесів. Використання експоненціальних кривих зростання передбачає, що майбутній розвиток залежить від досягнутого рівня, тобто, приріст залежить від значення функції.
В економіці використовуються два різновиди експоненціальних кривих: проста експонента і модифікована експонента.
Проста експонента може набувати різноманітних еквівалентних форм.
, основна форма . (3.2.12)
, b замінюємо на , де . (3.2.13)
, b замінюємо на (1-r), де . (3.2.14)
, де a замінюємо на , i b на . (3.2.15)
, де a замінюємо на , i b на , (3.2.16)
де а і b – додатні числа, при цьому якщо , то функція зростає, якщо – спадає.
Усі ці форми використовуються на практиці для описання різних економічних процесів, наприклад, форму (3.2.14) найчастіше використовують у фінансах, де r означає норму річного відсотка.
Логарифми ординат простої експоненти лінійно залежать від часу. Наприклад, для функції (3.2.12) , тобто темп зростання постійний для будь-якого моменту часу. Якщо ця крива застосовується для зображення інфляції, то коефіцієнт b буде характеризувати темп інфляції. Можна помітити, що ордината цієї функції змінюється з постійним темпом приросту. Якщо узяти відношення приросту до самої ординати, то воно буде сталою величиною: .
Модифікована експонента має вид
, (3.2.17)
де постійні величини: , , а константа має назву асимптоти цієї функції, тобто значення функції необмежено наближуються (знизу) до величини . Можуть бути й інші варіанти модифікованої експоненти, але на практиці найчастіше зустрічається розглянута вище функція. Наприклад, якщо на ринку з’являється новий товар, який супроводжується широкою рекламою, то спочатку попит на цей товар буде досить великий і швидкість продажу товару буде значною. З часом продаж буде стабілізуватися і дійде до певного рівня насичення. У таких випадках фаза уповільненого зростання відсутня і найкраще згладжування дасть модифікована експонента.
Логарифми перших приростів даної функції лінійно залежать від часу, а якщо узяти відношення двох послідовних приростів, то воно буде сталою величиною: .
Модифікована експонента служить базовою кривою, на основі якої за допомогою певних перетворень отримують криву Гомперця (3.2.23) і логістичну криву (3.2.24). які використовуються частіше.
Степенева крива. Рівняння степеневої кривої має вигляд
. (3.2.18)
Степенева крива добре згладжує показники, які з часом монотонно зростають, якщо , або спадають, якщо . Зокрема, при , . Це рівняння задає гіперболу, асимптотами якої є вісі координат, а добуток змінних є сталою величиною (). В економіці такій умові задовольняє крива попиту з одиничною еластичністю: відсоток збільшення одиниці часу t на такий самий відсоток зменшує залежну змінну . На практиці степеневі функції використовуються для зображення різноманітних економічних процесів. Найбільш відомою з них є виробнича функція Кобба-Дугласа. Крім того, вони застосовуються для зображення кривих байдужості, а також попиту на товари різних категорій (так звана крива Торнквіста) тощо.
Гіперболічна крива 1 типу. Звичайна гіпербола задається рівнянням
. (3.2.19)
Для цього типу гіперболи при значення зменшується із зростанням t і асимптотично наближується до а. Подібного виду крива може застосовуватися для вирівнювання і прогнозування показника, який з часом спадає до певного відмінного від нуля рівня.
При значення додатне, тільки якщо ; збільшення t приводить в цьому випадку і до збільшення з асимптотичною межею, що дорівнює а. Таким типом гіперболи доцільно зображувати зростаючі процеси із насиченням.
Гіперболічна крива II типу. Цей тип гіперболи задається рівнянням
(3.2.20)
При значення прагнуть до нуля при необмеженому збільшенні часу t; при значення прагне до нескінченності, якщо t наближується до a/b. Остання ситуація на практиці мало імовірна.
Гіперболічна крива IIІ типу (проста раціональна залежність). Задається рівнянням
. (3.2.21)
Для цього типу гіперболи незалежно від коефіцієнту b при t=0 =0. Для додатних значень b значення зростає і асимптотично прагне до величини 1/b при необмеженому збільшенні t. При від’ємному b ця крива, як і гіпербола другого типу, стає нестійкою при t = a/b.
S-подібна крива. В економіці досить розповсюджені процеси, які спочатку поступово зростають, прискорюються, а потім знов уповільнюють свій розвиток, прагнучи до певної межі. Наприклад, процес введення промислового об’єкта до експлуатації або коли змінюється попит на товари, що мають межу насичення тощо. Для моделювання таких процесів використовуються так звані S-подібні криві зростання, які мають вираз
(3.2.22)
Насправді ця крива має форму S тільки при від’ємному значенні b і за умов, що його абсолютне значення більше а. Якщо крива (3.2.22) дійсно має форму S, вона використовується для зображення повного циклу розвитку динамічних процесів. Повний цикл таких процесів починається з повільного зростання, потім наступає фаза бурхливого розвитку і, нарешті, розвиток закінчується періодом насичення (тобто асимптотичного наближення до величини ). Таке чергування фаз властиве багатьом соціально-економічним процесам. Для S-подібної кривої точкою перегину, в якій швидкість зростання досягає максимального значення, знаходиться через розв’язування рівняння , де – друга похідна по t кривої f(t). Для S-подібної кривої точкою перегину, тобто точкою, в якій зростання коефіцієнту нахилу дотичної змінюється спадом, буде точка . На практиці, однак, для описання таких процесів замість S-подібної кривої використовуються більш гнучкі і адекватні криві: Гомперця і логістична.
Крива Гомперця має наступний аналітичний вираз
, (3.2.23)
де с, b – додатні параметри, причому; параметр а – асимптота функції.
В кривій Гомперця виділяються чотири ділянки: на першій – приріст функції незначний, на другій – приріст збільшується, на третій ділянці – приріст майже постійний, на четвертій – відбувається уповільнення темпів приросту і функція необмежено наближається до значення а. В результаті конфігурація кривої нагадує латинську літеру S. Точкою перегину цієї кривої буде зі значенням функції , яке дорівнює , де е = 2,71828. Логарифм даної функції () є модифікованою експонентою; логарифм відношення першого приросту до самої ординати функції – лінійною функцією часу.
На основі кривої Гомперця будується, наприклад, динаміка показників рівня життя; модифікації цієї кривої використовуються у демографії для моделювання показника смертності тощо.
Логістична крива, або крива Перла-Ріда – зростаюча функція, найчастіше записується у вигляді
. (3.2.24)
У цьому виразі і – додатні параметри; – граничне значення функції при нескінченному зростанні часу.
Якщо взяти похідну від даної функції, то можна побачити, що швидкість зростання логістичної кривої у будь-який момент часу пропорційна досягнутому рівню функції і різниці між граничним значенням і досягнутим рівнем. Логарифм відношення першого приросту функції до квадрату її значення (ординати) є лінійна функція від часу.
Конфігурація графіка логістичної кривої близька до графіка кривої Гомперця, але на відміну від останнього логістична крива має точку симетрії, яка співпадає із точкою перегину. Точка перегину дорівнює . Значення у точці перегину дорівнює .
Метод найменших квадратів і процедури регресійного аналізу повністю підходять для випадку, коли рівняння кривої зростання після деяких перетворень може бути зведено до лінійної регресії. В таблиці 3.2.1. наведені криві зростання, які найчастіше спостерігаються в соціально-економічних дослідженнях, їх математичні функції та перетворення, необхідні для зведення функцій до лінійного вигляду.
Таблиця 3.2.1
Види кривих зростання
| Основні види кривих зростання | Математична
функція |
Лінеаризація функції |
| 1 | 2 | 3 |
| Лінійна (поліном першого ступеня) | Не потрібна | |
| Квадратична (поліном другого ступеня) | ||
| Поліном третього ступеня | ||
| Експонента (проста) | ||
| Логарифмічна крива | ||
| S-подібна крива | ||
| Обернена логарифмічна крива | , | |
| Степенева | ||
| Гіперболічна крива І типу | ||
| Гіперболічна крива ІІ типу | , | |
| Гіперболічна крива ІІІ типу | , , | |
| Модифікована експонента | ;
; . |
|
| Крива Гомпертця | ||
| Логістична крива | = | , |
Як видно з таблиці 3.2.1 в практиці криволінійного вирівнювання широко використовуються два види перетворень: логарифмування () і зворотне перетворення (). При цьому можливі перетворення як залежної змінної , так і незалежної t або одночасно і тієї й іншої. Параметри S-подібних кривих (Гомпертця і логістичної кривої) визначаються більш складним способом. Вони можуть бути одержані з модифікованої експоненти, так само, як були одержані зі звичайної лінійної регресії криві, розглянуті раніше. Криві, побудовані за модифікованою експонентою, задаються трьома параметрами (замість двох параметрів у лінійній залежності). Спочатку визначається параметр с, а потім два інших параметри: а і b. В табл. 3.2.1 наведені відповідні перетворення функції Гомпертця і логістичної кривої у модифіковану експоненту.
Апроксимація спостережень складними функціями дає задовільне наближення до фактичних спостережень, але зменшує стійкість моделі на інтервалі упередження прогнозу. Тому використовувати для прогнозування такі моделі (наприклад, поліном вище другого ступеня) слід обережно. В комп’ютерних програмних засобах використовують до двох десятків моделей. Зазначимо, що пошук параметрів функції Гомпертця і логістичної кривої, через неможливість їх лінеаризації, ведеться методом багатомірної числової оптимізації.
Вибір кривої зростання. Правильно встановити вид кривої, тобто вид аналітичної залежності значення показника від часу – одна з найважчих задач. Обрана функція тренду повинна задовольняти наступним умовам: бути теоретично обґрунтованою; мати якнайменшу кількість параметрів; параметри функції повинні мати економічне тлумачення; оцінені значення тренду повинні якомога менше відрізнятися від відповідних фактичних спостережень часового ряду.
Вибір форми кривої для згладжування в певній мірі залежить від мети згладжування: інтерполяції або екстраполяції. У першому випадку метою є досягнення найбільшої близькості до фактичних рівнів часового ряду. У другому – виявлення основної закономірності розвитку явища, стосовно якої можна припустити, що в майбутньому вона збережеться.
В основі вибору кривої лежить теоретичний аналіз сутності економічного явища, зміни якого відображаються часовим рядом. Іноді до уваги беруться міркування про характер зростання рівнів ряду. Так, якщо зростання випуску продукції передбачається у вигляді арифметичної прогресії, то згладжування відбувається за прямою, Якщо ж зростання йде в геометричній прогресії, то згладжування виконується за показниковою функцією.
На практиці, під час попереднього аналізу часового ряду відбирають, як правило, дві-три криві зростання для подальшого дослідження і побудови трендової моделі часового ряду. Розглянемо проблему вибору виду кривої зростання для конкретного часового ряду.
Метод послідовних різниць (Тінтнера). Цей метод може бути використаний для визначення порядку (ступеня) апроксимуючого поліному, якщо, по-перше, рівні часового ряду складаються тільки із двох компонент: тренду і випадкової, і по-друге, тренд є досить гладким, щоб його можна було згладити поліномом певного ступеня. Алгоритм застосування методу ідентичний алгоритму визначення порядку інтеграції нестаціонарного процесу (див. 2.6) і складається з наступних кроків.
- Розраховуються різниці (прирости) до d-гo порядку включно:
;
; (3.2.25)
. . . . . . . . . .
.
Для апроксимації економічних процесів як-правило розраховують різниці до четвертого порядку.
- Для вхідного ряду і для кожного різницевого ряду обчислюють дисперсії за наступними формулами:
для вхідного ряду – ; (3.2.26)
для різницевого ряду d-го порядку (d = 1,2, …) – , (3.2.27)
де – біноміальний коефіцієнт.
- Порівнюються значення кожної наступної дисперсії з попередньою, тобто розраховуються різниці , і якщо для будь-якого k ця величина не перевищує певної наперед заданої додатної величини, тобто порядок величин дисперсій однаковий, то ступінь апроксимуючого поліному повинна дорівнювати d – 1.
Необхідно зазначити, що для визначення тренду в економічних часових рядах не слід використовувати поліноми дуже великого порядку, оскільки отримані таким чином функції згладжування будуть відображати випадкові відхилення, а не детерміновану складову, що суперечить поняттю тенденції.
Метод характеристик приросту є універсальним методом попереднього вибору кривих зростання. Він заснований на використанні окремих характерних властивостей кривих, розглянутих вище. При цьому методі вхідний часовий ряд попередньо згладжується методом простої ковзної середньої. Наприклад, для інтервалу згладжування т=3 згладжені рівні розраховуються за формулою
, (3.2.28)
причому щоб не втратити перший і останній рівні, їх згладжують за формулами
, . (3.2.29)
Далі розраховуються перші середні прирости
, t=2,3,…l,n-1; (3.2.30)
другі середні прирости
, (3.2.31)
а також ряд похідних величин:
; ; ; . (3.2.32)
Відповідно до характеру зміни середніх приростів і похідних показників вибирається вид кривої зростання для вхідного часового ряду [27], при цьому використовуються відомості з табл. 3.2.2.
Таблиця 3.2.2.
Вибір кривої зростання за характером зміни показника.
| Показник | Характер зміни показника з часом | Вид кривої зростання |
| Перший середній приріст | Майже однаковий | Поліном першого порядку (пряма) |
| Другий середній приріст | Змінюється лінійно
Змінюється лінійно |
Поліном другого порядку (парабола)
Поліном третього порядку (кубічна парабола) |
| Майже однаковий | Проста експонента | |
| Змінюється лінійно | Модифікована експонента | |
| Змінюється лінійно | Крива Гомпертця | |
| Змінюється лінійно | Логістична крива |
3.3 Прогнозування тенденції часового ряду за алгоритмічними методами.
Суть алгоритмічних методів полягає у послідовній заміні фактичних рівнів часового ряду їх згладженими значеннями , які за певним алгоритмом розрахунку оцінюють невідому функцію тренду у будь-якій наперед заданій точці , не претендуючи при цьому на аналітичне (тобто у вигляді певної формули) представлення функції для усього базового періоду . Вони мають механізм автоматичного настроювання на зміну досліджуваного показника. Завдяки цьому, модель постійно пристосовується до зміни інформації і в кінці інтервалу прогнозної бази відображає тенденцію, яка склалася на поточний момент. Прогноз отримується як екстраполяція тенденції поточного рівня ряду, тобто останнього на даний момент.
Найбільш відомими ітераційними методами згладжування часових рядів є метод ковзної середньої, експоненціального згладжування, адаптивного згладжування та їх модифікації.
Метод ковзної середньої (– “moving average”). Цей метод є одним з найпростіших методів виділення тренду. Згладжування за допомогою ковзної середньої засноване на тому, що в середніх величинах взаємно гасяться випадкові відхилення. Саме зменшення випадкового розкиду (дисперсії) якраз і означає згладжування відповідної траєкторії.
Згладжування за допомогою ковзної середньої відбувається наступним чином. Початкові рівні часового ряду замінюються його середніми (згладженими) величинами , розрахованими для певної кількості рівнів ряду. Одержані значення відносяться до середини обраного інтервалу. Потім інтервал зсувається на одне спостереження і розрахунок повторюється. Інтервали визначення середньої беруться весь час однаковими. Таким чином у кожному інтервалі згладжена середня оцінює середню точку цього інтервалу. В процесі згладжування часового ряду ковзною середньою участь в розрахунках приймають усі рівні ряду. Чим ширший інтервал ковзання, тим гладкішим виглядає тренд. Кількість даних, які входять в інтервал, називають порядком ковзної середньої. Наприклад, якщо в інтервал згладжування входять т значень часового ряду, то ми маємо ковзну середню -го порядку, що записується, як .
Приклад 3.3.1. На рис.3.3.1 зображено згладжування часового ряду щомісячних змін реального ВВП за п’ять років відповідно ковзними середніми порядку 4, 9, І2 та 15. Очевидно, що з підвищенням порядку згладжування ряд стає гладкішим. Для ковзної середньої 12-го порядку він навіть більш гладкий, ніж для ковзної середньої 15-го порядку. Такий ефект пов’язаний з наявністю сезонності в часовому ряду, причому період сезонних коливань збігається з інтервалом згладжування.
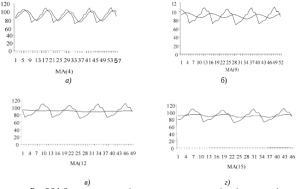
Рис. 3.3.1. Згладжування динамічного ряду ковзними середніми різних порядків.
Вибір інтервалу згладжування залежить від специфіки вхідних даних. Окрім того, з його обранням пов’язане питання про техніку розрахунку ковзної середньої. Розраховані середні дані потрібно розміщувати в центрі інтервалу згладжування. При цьому, якщо непарне, то розрахована середня попадає в центр інтервалу згладжування на фактично існуючий рівень часового ряду. Якщо – парне, то розраховану середню не можна віднести до жодного рівня ряду: вона буде розташована у центрі інтервалу між двома суміжними рівнями. Для того, щоб уникнути цієї незручності, додатково розраховують центровані ковзні середні (МAС) цих двох суміжних ковзних середніх.
Нехай непарний інтервал можна представити як (ціле число обирають відповідно до нерівності і, як правило, не перевищує трьох). Тоді для непарного ковзна середня розраховується за формулою:
= . (3.3.1)
Наприклад, ковзна середня 7-го порядку в період t матиме вигляд:
, т=7, =3 i 3<t< п-2.
Якщо – парне і його можна подати у вигляді (2), ковзна середня розраховується за формулою:
= . (3.3.2)
Наприклад, ковзна середня 6-го порядку дорівнює:
, т=6; =3; 3<t< п-2.
Зазначимо, що якщо часовий ряд є періодичним з періодом сезонності , тобто , то яким би не було t, = const. Ковзна середня 12-го порядку згладжує більшість сезонних коливань.
Розрахунок ковзних середніх відбувається доти, доки не буде розраховано згладжене значення для останнього інтервалу згладжування заданого часового ряду. В результаті будуть знайдені оцінки згладжених значень часового ряду для всіх , окрім та . Отже, згладжений ряд коротший за початковий на () спостережень. Для визначення згладжених значень у перших й останніх крайніх точках усього часового ряду можна використати відповідні значення локально апроксимуючих поліномів, побудованих, відповідно, за першими й останніми точками часового ряду .
Оцінка дисперсії ковзної середньої дорівнює
, (3.3.3)
де – оцінка дисперсії усіх членів вхідного ряду.
Прогнозованому значенню на один період упередження відповідає останнє згладжене значення , яке було розраховане як ковзна середня -го порядку (як парного, так і непарного ) за останніми даними часового ряду . Зазначимо, що згладжене значення у випадку стаціонарного ряду дорівнює прогнозу очікуваного значення показника в майбутньому не тільки на прогнозований період , а й на наступний період і далі.
Точніші результати згладжування дає застосування зваженої ковзної середньої. Її оцінка в середині кожного інтервалу згладжування описується поліномом -го ступеня:
. (3.3.4)
Параметри цього рівняння знаходять за методом найменших квадратів. Зважену ковзну середню у обраному інтервалі визначають як середній член згладжених за поліномом (3.3.4) рівнів часового ряду.
Наприклад, якщо в інтервал згладжування входять п’ять спостережень, а тенденція може бути представлена поліномом другого ступеня, то згладжений середній рівень у взятому інтервалі буде виражати значення тенденції на початку відліку. При початок відліку, як виходить з формули (3.3.4), дорівнює .
Для цього випадку
, (3.3.5)
де коефіцієнти при (позначимо їх ) характеризують “вагу”, що надається рівню ряду розташованому на відстані від моменту . Наприклад, .
Розраховані таким чином ваги мають дві основні властивості: сума ваг дорівнює одиниці (цим процедура ковзної середньої, дещо відрізняється від поняття МА-процесів, введеного у розділі 2.2, оскільки підсумок коефіцієнтів () у (2.2.1) не обов’язково дорівнює одиниці); ваги симетричні по відношенню до середньої величини інтервалу згладжування.
Вказані властивості характерні для будь-якої системи ваг, що розраховується за зваженою ковзною середньою. Розраховані значення вагових коефіцієнтів , для різної довжини відрізків усереднення (або порядку згладжування ) і порядку апроксимуючого поліному (3.3.2) наведені в таблиці 3.3.1 [24]. Зазначимо, що, по-перше, значення для додатних не наводяться, оскільки коефіцієнти симетричні відносно середини відрізка згладжування, тобто =; по-друге, при однаковій довжині інтервалів згладжування , ваги у формулі (3.3.4) для поліномів парного ступеня будуть такими ж самими, що й для поліномів ступеня більшого на одиницю (непарного).
Таблиця 3.3.1.
Значення вагових коефіцієнтів в залежності від довжини відрізків усереднення та порядку апроксимуючих поліномів
| w-k | w-k+1 | … | w0 | ||
| 0 або 1 | … | ||||
| 5 | 2 або 3 | – | |||
| 7 | 2 або 3 | ||||
| 9 | 2 або 3 | ; | |||
| 7 | 4 або 5 | ||||
| 9 | 4 або 5 | ; |
Метод ковзної середньої набув поширення для короткострокового прогнозування. Згладжування часових рядів за допомогою ковзної середньої дозволяє наочно визначити вид тренду. При більших значеннях коливання згладженого ряду помітно зменшується, але одночасно значно скорочується кількість спостережень. Цей недолік помітний при невеликій довжині ряду, або якщо необхідно зробити екстраполяцію на майбутнє. Окрім того, тренд, одержаний за допомогою ковзної середньої, не має кількісного виразу, тобто швидкість зміни ряду не відома. При невеликій кількості спостережень метод часто приводить до викривлення тенденцій, а вибір величини інтервалу згладжування важко буває обґрунтувати, хоча від цього залежить форма кривої. Одночасно зі зменшенням дисперсії у згладженому ряду можуть з’явитися систематичні коливання, обумовлені автокореляцією його послідовних значень аж до порядку (ефект Слуцького-Юла), тобто методи ковзної середньої можуть спричинити автокореляцію залишків, навіть якщо вона була відсутня у початкових даних..
8Приклад 3.3.1. У таблиці 3.3.2 наведена динаміка основних індексів цін (ІЦ%) за дванадцять кварталів: з 1кв.1999р. по 4кв.2001р. Згладимо наведені дані простою ковзною середньою 4-го порядку (МA(4)) і визначимо прогноз ІЦ на 1кв.2002р.
Таблиця 3.3.2
| Квартали | t | ІЦ | Разом за 4 квартали | Ковзні середні МA(4) | Центровані ковзні середні МAС(2) | Прогноз | Похибки |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1999 1кв. | 1 | 105,8 | |||||
| 2кв. | 2 | 105,0 | |||||
| 417,6 | 104,40 | ||||||
| 3кв. | 3 | 101,0 | 105,125 | ||||
| 423,4 | 105,85 | ||||||
| 4кв. | 4 | 105,8 | 106,0875 | ||||
| 425,3 | 106,33 | ||||||
| 2000 1кв. | 5 | 111,6 | 106,6875 | 104,40 | 7,2 | ||
| 428,2 | 107,05 | ||||||
| 2кв. | 6 | 106,9 | 106,825 | 105,85 | 1,05 | ||
| 426,4 | 106,6 | ||||||
| 3кв. | 7 | 103,9 | 105,5625 | 106,33 | -2,43 | ||
| 418,1 | 104,53 | ||||||
| 4кв. | 8 | 104,0 | 103,9875 | 107,05 | -3,5 | ||
| 413,8 | 103,45 | ||||||
| 2001 1кв. | 9 | 103,3 | 102,8125 | 106,6 | -3,3 | ||
| 408,7 | 102,18 | ||||||
| 2кв. | 10 | 102,6 | 101,8375 | 104,53 | -1,93 | ||
| 406,0 | 101,5 | ||||||
| 3кв. | 11 | 98,8 | 103,45 | -4,65 | |||
| 4кв. | 12 | 101,3 | 102,18 | -0,88 | |||
| 2002 1кв. | 13 | 101,5 |
Порядок згладжування ряду:
- обчислюємо середнє за перші чотири квартали:
105,8 + 105,0 + 101,0 + 105,8 = 417,6;
- отримане загальне середнє ділимо на 4. Звідси – перша ковзна середня дорівнює 104,4;
- цю середню вміщуємо в середню дату, між 2 та 3 кварталами.
Потім інтервал згладжування зсувається на один рівень униз, повторюється розрахунок середньої арифметичної тощо. Згладжений ряд наведено в п’ятому стовпчику таблиці. Як бачимо, довжина згладженого ряду справді зменшується на (–1)=3.
Для наведеного вище прикладу застосування центрованої ковзної середньої 2-го порядку дозволяє розташувати дані згідно з існуючими кварталами спостережень часового ряду.
Прогнозоване значення показника на момент часу =13 розраховується як ковзна середня 4–го порядку для 4-х останніх рівнів часового ряду .
.
Різниці між вхідним рядом та прогнозними значеннями дорівнюють оцінкам похибок прогнозу. 8
Метод експоненціального згладжування. Метод експоненціального згладжування дає можливість описати такий розвиток процесу, коли найбільша вага надається останньому спостереженню, а вага решти спостережень спадає геометрично. Одержана в результаті середня більше характеризує значення процесу наприкінці інтервалу згладжування, ніж на початку і відома як експоненціально зважена середня. Так, для спостережень , прогноз наступного значення має вид:
, , (3.3.6)
де підсумок усіх ваг дорівнює 1, а – має назву параметр згладжування.
Практичний розрахунок експоненціальної середньої здійснюється за рекурентною формулою:
або , (3.3.7)
тобто у розрахунку нової експоненціальної середньої береться попередня експоненціальна середня та доля () від різниці між минулим спостереженням та його згладженим значенням, тобто похибки . Так, із надходженням нового спостереження розраховується прогноз , як експоненціальна середня наступного значення ; параметр обирається при цьому з умови мінімуму похибки прогнозу.
Можна показати, що математичні сподівання часового ряду та експоненціально згладженого ряду однакові, а дисперсія згладжених рівнів стає меншою за дисперсію початкового ряду спостережень:
, , (3.3.8)
тобто якщо наближається до одиниці, то різниця між дисперсіями невелика, однак зі зменшенням коливання експоненціальної середньої стають більш гладкими. Тим самим експоненціальна середня відіграє роль фільтру, який поглинає коливання часового ряду.
Процедура оцінювання стандартної похибки прогнозу може здійснюватися також за методом експоненціального згладжування. Якщо похибка прогнозу оцінюється як різниця між фактичним й прогнозним значенням , то замість обчислення суми квадратів похибок і знаходження дисперсії, застосуємо інший вимір розкиду, відомий під назвою середнє абсолютне відхилення похибки (MADt) (Див. (7.1)). Одним із різновидів експоненціально зваженого середнього може бути експоненціально зважена середня абсолютних похибок прогнозу:
. (3.3.9)
Для досить великого класу статистичних розподілів значення середнього квадратичного відхилення дещо перевищує значення середнього абсолютного відхилення і строго пропорційне йому. Константа пропорційності для різних розподілів коливається між 1,2 та 1,3 (для нормального закону розподілу це значення дорівнює =1,2533), тому
=. (3.3.10)
Використання методу експоненціального згладжування передбачає вирішення трьох питань: вибір постійної згладжування , вибір початкового рівня згладжування ряду , вибір початкового моменту згладжування (довжини, бази згладжування). Аналітичного розв’язку поставлених задач на сьогоднішній день не існує, та і він навряд чи можливий. Вибір характеристик згладжування повинен бути оснований на експериментальних розрахунках і здійснюватися у кожному конкретному випадку по-різному.
Вибір постійної згладжування. Вибір параметра згладжування є основною і досить складною проблемою. Для різних значень результати прогнозування будуть відрізнятися. Якщо значення близьке до одиниці, то при прогнозуванні враховується в основному вплив останніх спостережень; якщо близьке до нуля – то вплив рівнів ряду, спадає повільно, що дозволяє врахувати минулі значення.
Для розв’язання практичних завдань часто використовують різноманітні емпіричні процедури. Наприклад, можна вибирати константу згладжування шляхом мінімізації похибок прогнозу, які оцінюються для останньої третини ряду, використовуючи наступну ітеративну процедуру:
- Вибрати одну із характеристик оцінки якості прогнозу (див. (7.1)), наприклад: MSE, МАЕ, МАРЕ тощо.
- Розділити множину визначення параметра на значення, які змінюються з певним кроком, наприклад з кроком 0,1. Тоді маємо підмножину значень , яка дорівнює: [0; 0,1; 0,2; …; 0,9; 1].
- Вибрати початкове наближення, наприклад =.
- Для кожного значення із побудованої підмножини провести розрахунок експоненціально згладжених середніх.
- Розрахувати значення обраної характеристики якості прогнозу.
- Вибрати , для якого характеристика якості прогнозу вийшла найкращою.
Аналогічно можна підібрати і довжину прогнозної бази, і початковий рівень згладжування .
Вибір початкового рівня згладжування ряду . Від вибору початкового рівня згладжування залежить поведінка наступної згладженої послідовності. Найчастіше він або дорівнює значенню першого рівня ряду , або береться на рівні середньої арифметичної ряду. Можна скористатися спеціальними формулами, розробленими Брауном [].
Зазначимо, що чим довший ряд, тим менший вплив на результат згладжування спричиняє вибір .
Вибір початкового моменту згладжування (довжини бази згладжування). Проблема вибору початкової точки згладжування походить від проблеми вибору сталої згладжування . Чим ближче початкова точка до поточної, тим менше інформації знадобиться для побудови прогнозу і тим ближче до 1; чим далі початкова точка до поточної, тим менш чутливим буде прогноз до нових даних, що надходять, і тим ближче до 0.
Метод експоненціального згладжування застосовується у короткостроковому прогнозуванні. Для побудови прогнозу необхідно задати лише початкову оцінку прогнозу, подальші розрахунки здійснюються автоматично із надходженням нових даних спостережень і не потрібно обчислювати прогноз починаючи спочатку. За цим методом згладжування не втрачаються ні початкові, ні останні рівні заданого часового ряду і тут немає точки, на якій ряд обривається. Чутливість експоненціально зваженого середнього з метою підвищення адекватності прогнозної моделі може бути в будь-який час змінена, якщо зробити іншою величину .
8 Приклад 3.3.2. За даними таблиці 3.3.3 зробити прогноз доходу бюджету України, використовуючи метод простого експоненціального згладжування.
Розв’язування. Задамо початкове згладжене значення Iкв.1999 на рівні 24,775 %, тобто на рівні середнього значення показника за всі періоди спостережень, і величину за двома варіантами: =0,7 i =0,35. Обчислюємо прогноз на II кв. 1999р. (=0,7):
IIкв.1999 = 0,7∙23,8 + 0,3∙25,219 = 24,226 %.
Таблиця 3.3.3
| Періоди | № кварталу | Доходи бюджету
у % ВВП () |
Прогноз () | Похибка прогнозу | Прогноз () | Похибка прогнозу |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Січень-Березень 1999 | 1 | 23,8 | 25,21875 | -1,41875 | 25,21875 | -1,41875 |
| Квітень-Червень | 2 | 25,3 | 24,225625 | 1,074375 | 24,72219 | 0,577813 |
| Липень-Вересень | 3 | 22,5 | 24,977688 | -2,47769 | 24,92442 | -2,42442 |
| Жовтень-Грудень | 4 | 26,6 | 23,243306 | 3,356694 | 24,07587 | 2,524126 |
| Січень-Березень 2000 | 5 | 26,1 | 25,592992 | 0,507008 | 24,95932 | 1,140682 |
| Квітень-Червень | 6 | 27,2 | 25,947898 | 1,252102 | 25,35856 | 1,841443 |
| Липень-Вересень | 7 | 25,3 | 26,824369 | -1,52437 | 26,00306 | -0,70306 |
| Жовтень-Грудень | 8 | 31 | 25,757311 | 5,242689 | 25,75699 | 5,24301 |
| Січень-Березень 2001 | 9 | 26,8 | 29,427193 | -2,62719 | 27,59204 | -0,79204 |
| Квітень-Червень | 10 | 25,2 | 27,588158 | -2,38816 | 27,31483 | -2,11483 |
| Липень-Вересень | 11 | 23,2 | 25,916447 | -2,71645 | 26,57464 | -3,37464 |
| Жовтень-Грудень | 12 | 24,4 | 24,014934 | 0,385066 | 25,39351 | -0,99351 |
| Січень-Березень 2002 | 13 | 24,9 | 24,28448 | 0,61552 | 25,04578 | -0,14578 |
| Квітень-Червень | 14 | 24,4 | 24,715344 | -0,31534 | 24,99476 | -0,59476 |
| Липень-Вересень | 15 | 22,1 | 24,494603 | -2,3946 | 24,78659 | -2,68659 |
| Жовтень-Грудень | 16 | 24,7 | 22,818381 | 1,881619 | 23,84629 | 0,853714 |
| Січень-Березень 2003 | 17 | 24,14509 | ||||
| Квітень-Червень | 18 | 23,60431 | ||||
| Липень-Вересень | 19 | 23,46280 | ||||
| Жовтень-Грудень | 20 | 22,70582 | ||||
| RMSE = | 2,265137 | RMSE = | 2,136995 |
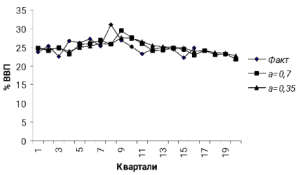
Рис.3.3.2. Фактичні та прогнозовані значення доходу бюджету України.
Прогнози на наступні квартали 1999-2002 років розраховуються аналогічно. Оскільки значення за I квартал 2003 року невідоме, всі прогнози на більш віддалене майбутнє дорівнюють прогнозу на Iкв.2003 р.
Згладжені ряди у стовпчиках 4 та 6 побудовані на основі різних , але однакового початкового прогнозу. Розрахуємо похибки двох одержаних прогнозів за показником RMSE=. Значення RMSE за 1999-2002 роки істотно не відрізняються але слід віддати перевагу значенню =0,35, за яким прогноз має меншу похибку (RMSE = 2,14). Значення точкових прогнозів на чотири квартали наступного року розраховані у стовпчику 6. На рис.2.2.2 побудовані графіки фактичних та прогнозних значень доходів бюджету.
Для розрахунку інтервального прогнозу знайдемо оцінку стандартної похибки згладженого ряду за формулою (3.3.10). Абсолютні значення похибок прогнозу, їх експоненціально зважені середні () та стандартні похибки прогнозу наведені в наступній таблиці. Виходячи з припущення про незалежність похибок та нормальний їх розподіл можна сподіватися, що значення фактичного доходу бюджету в січні-березні 2003 року буде знаходитися в інтервалі .
Таблиця 3.3.4
| № кварталу | Прогноз () | |||
| 1 | 25,21875 | 1,419 | 2,522 | 3,152 |
| 2 | 24,72219 | 0,578 | 2,136 | 2,670 |
| 3 | 24,92442 | 2,424 | 1,590 | 1,988 |
| 4 | 24,07587 | 2,524 | 1,882 | 2,353 |
| 5 | 24,95932 | 1,141 | 2,107 | 2,634 |
| 6 | 25,35856 | 1,841 | 1,769 | 2,211 |
| 7 | 26,00306 | 0,703 | 1,794 | 2,243 |
| 8 | 25,75699 | 5,243 | 1,412 | 1,765 |
| 9 | 27,59204 | 0,792 | 2,753 | 3,441 |
| 10 | 27,31483 | 2,115 | 2,067 | 2,583 |
| 11 | 26,57464 | 3,375 | 2,084 | 2,604 |
| 12 | 25,39351 | 0,994 | 2,535 | 3,169 |
| 13 | 25,04578 | 0,146 | 1,996 | 2,495 |
| 14 | 24,99476 | 0,595 | 1,348 | 1,685 |
| 15 | 24,78659 | 2,687 | 1,085 | 1,356 |
| 16 | 23,84629 | 0,854 | 1,645 | 2,057 |
| 17 | 24,14509 | 1,368 | 1,710 | |
| 18 | 23,60431 | 0,889 | 1,112 | |
| 19 | 23,46280 | 0,578 | 0,723 | |
| 20 | 22,70582 | 0,376 | 0,470 |
8
Адаптивні методи прогнозування часових рядів. Адаптивне прогнозування дозволяє автоматично змінювати константу згладжування в процесі обрахунку. Інструментом прогнозування в адаптивних методах є математична модель з одним чинником «час».
Адаптивні моделі прогнозування – це моделі дисконтування даних, які здатні швидко пристосовувати свою структуру й параметри до зміни умов. Найважливіша їх особливість полягає в тому, що це саморегулюючі моделі і при появі нових даних прогнози оновлюються з мінімальною затримкою без повторення всього обсягу обчислень спочатку.
Нехай ми знаходимося в якомусь поточному стані, для якого відомий попередній рівень ряду та очікуване значення . В залежності від закладеної в модель гіпотези формування сподіваних значень розрізняють моделі адаптивних сподівань, неповного коригування, раціональних сподівань. Методи розрахунку досить складні, розглянемо лише підхід до цієї проблеми. Схема такого процесу представлена на рис.1.
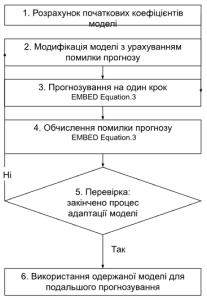
Рис.1. Схема побудови адаптивних моделей
При надходженні фактичного значення обчислюється помилка, розбіжність між прогнозованим і фактичним рівнем (довгострокова функція моделі): .
В моделі передбачається, що зміна фактичного рівня є деякою часткою () від очікуваної зміни . Параметр називається коригуючим коефіцієнтом або параметром адаптації. За критерій оптимальності при виборі параметру адаптації може бути узятий мінімум середнього квадрату помилок прогнозування. Чим ближчий до одиниці, тим більш сподівання економічних суб’єктів відповідають реальній динаміці часового ряду, і навпаки, чим ближче до нуля – тим менш володіємо ситуацією і треба вносити корективи.
Помилка прогнозу через обернений зв’язок надходить в модель і враховується в залежності з прийнятою системою переходу від одного стану в наступний. В результаті з’являються “компенсаційні” зміни, які дозволяють коригувати параметри моделі з метою більшого узгодження поведінки моделі з динамікою ряду. Наприклад, для лінійного тренду , експоненціальна середня першого порядку буде модифікована у модель: . Дане співвідношення називають короткостроковою функцією моделі.
Потім розраховується прогноз на наступний період, і процес повторюється знову. Таким чином, адаптація здійснюється ітеративно з одержанням кожної нової фактичної точки ряду. Модель постійно “всмоктує” інформацію і розвивається з урахуванням нових тенденцій, які існують на теперішній момент часу. Завдяки відміченим властивостям адаптивні методи особливо успішно використовуються для оперативного прогнозування.
В практиці статистичного прогнозування базовими адаптивними моделями вважаються моделі Брауна і Хольта, які відносяться до схеми ковзної середньої, та модель авторегресії. Усі інші адаптивні методи (метод адаптивної фільтрації (МАФ), метод гармонічних ваг тощо [27]) розрізняються між собою способом оцінювання параметрів моделі та визначенням параметрів адаптації базових моделей.
Метод адаптивного згладжування Брауна. Метод Брауна є узагальненням методу простого експоненціального згладжування.
Розглянемо постановку задачі експоненціального згладжування в загальному випадку. Нехай часовий ряд () можна описати моделлю виду , де – функція тренду, – випадкові взаємонезалежні похибки із нульовим середнім значенням і сталою дисперсією, що розподілена нормально із нульовим математичним сподіванням і дисперсією .
У свою чергу, функцію можна розкласти в ряд Тейлора, тобто описати поліномом -го порядку
. (3.3.11)
Потрібно за даними ряду зробити прогноз на моменти часу () () шляхом зважування спостережень ряду так, щоб пізнішим спостереженням надати більшу вагу ніж попереднім. Прогноз рівнів ряду на період часу , де може бути побудований теж за допомогою розкладення в ряд Тейлора:
, (3.3.12)
де – -та похідна, узята в момент t.
Згідно з теоремою, доведеною Р Брауном та Р.Майєром будь-яка -та похідна () рівняння (3.3.11) може бути виражена через лінійні комбінації експоненціальних середніх до () порядку. Основною метою експоненціального згладжування при цьму є обчислення рекурентних виправлень до оцінок коефіцієнтів рівняння виду (3.3.11).
Так, експоненціальна середня 1-го порядку для ряду записується, як
, (3.3.13)
де – параметр згладжування ().
Експоненціальна середня -го порядку для ряду записується, як
. (3.3.14)
Для визначення експоненціальної середньої використовується наступна рекурентна формула:
. (3.3.15)
Тобто у розрахунку нової експоненціальної середньої береться попередня експоненціальна середня та частка () від різниці між новим спостереженням і попереднім його згладженим значенням.
Покажемо, як розраховується експоненціальна середня для моменту часу із раніш згладжених величин. Візьмемо, наприклад, експоненціальну середню першого порядку:
3.3.16)
Тут – величина, що характеризує початкові умови.
Отже, функція (3.3.15) є лінійною комбінацією усіх минулих спостережень. Ваги, які надаються минулим рівням , зі збільшенням спадають за геометричною прогресією. Тому коефіцієнт можна тлумачити як коефіцієнт дисконтування, який характеризує ступінь знецінення інформації з плином часу, а – як вагу поточного спостереження .
Наприклад, якщо параметр згладжування , то для моменту часу () вага для відповідного спостереження буде дорівнювати 0,3(1-0,3)=0,21; для спостереження в момент () вага становитиме 0,3(1-0,3)2=0,147; для моменту () – відповідно 0,1029 тощо.
Виходячи із рекурентної формули, можуть бути отримані експоненціальні середні різних порядків:
(3.3.17)
де – експоненціальна середня -го порядку в точці .
Знаючи експоненціальні середні різних порядків, можна визначити оцінки параметрів в розкладенні (3.3.11) і, відповідно, прогнозні значення рівнів динамічного ряду.
Метод експоненціального згладжування можна узагальнити на випадки будь-якого ступеня поліному для вираження невипадкової складової часового ряду але, як свідчить досвід, перевищення другого ступеня поліному не стільки збільшує точність прогнозу, як значно ускладнює процедуру розрахунків. Тому в основному розглядають три моделі Брауна:
Модель нульового порядку описує часовий ряд , в якому відсутні тренд та сезонні коливання і процес (3.3.11) представляється у вигляді
, (3.3.18)
де – невідомий незалежний від часу параметр, що характеризує поточний рівень ряду.
Модель першого порядку описує лінійну тенденцію
, (3.3.19)
де – параметр, значення якого характеризує середню останнього рівня ряду; – параметр, що характеризує приріст наприкінці періоду спостереження, а також (хоча в меншій мірі) швидкість зростання на більш ранніх періодах.
Модель другого порядку описує параболічну тенденцію із змінюваними швидкістю та прискоренням:
, (3.3.20)
де – параметр, значення якого характеризує поточний приріст або прискорення.
Зазначимо, що розглянуті моделі експоненціального згладжування різних порядків можна представити як окремі випадки -моделі. Припустимо, що похибки прогнозу є незалежними й однаково розподіленими. Тоді, підставляючи у (3.3.15) для експоненціальної середньої першого порядку матимемо модель: . Оскільки: , то остаточно, модель запишеться, як: . Підставляючи замість та позначивши , одержимо: , тобто прийшли до моделі або, якщо початковий ряд представити за допомогою оператора перших різниць L: , маємо -модель: .
Модель лінійно-адитивного тренду можна представити -моделлю:
з коефіцієнтами ковзної середньої – та .
Порядок моделі прийнято визначати або на основі візуального аналізу графіка процесу (чи існує тренд і чи близький він до лінійної функції), знаннях законів розвитку характеру зміни досліджуваного явища, або методом випробувань, порівнюючи статистичні характеристики моделей різного порядку на ділянці ретроспективного прогнозу.
Оцінювання параметрів моделей на кожному кроці прогнозування t () здійснюється за так званими формулами “оновлювання” (див. табл.3.3.5), які використовують похибку прогнозу, обчислену в момент часу () на один крок вперед (). Початкові значення параметрів моделей можна визначити за методом найменших квадратів, використовуючи декілька перших спостережень. Оптимальне значення коефіцієнту дисконтування знаходиться в межах [0;1], визначається методом числової оптимізації і не змінюються для усього періоду спостережень.
Точковий прогноз розраховується після підстановки значення в оцінену модель. Границі інтервалу надійності прогнозу можуть бути визначені за формулою []:
, (3.3.21)
де величини розраховуються індивідуально для моделей різних порядків (формули розрахунку наведені у табл. 3.3.5).
► Приклад 3.3.3. Побудувати прогноз кількості населення в Україні за лінійною моделлю Брауна. Ряд містить 24 рівня спостережень даного показника (Табл.3.3.6).
Скористаємося схемою адаптивного прогнозування. Початкові оцінки параметрів одержимо МНК за першими п’ятьма точками: 49638,7, 126,07.
Візьмемо , а параметр згладжування =0,3. В табл.3.3.6. наведені розрахунки параметрів моделі Брауна на кожному кроці. На останньому кроці одержуємо модель = 48455,66 – 645,443. Прогнозовані оцінки за цією моделлю розраховуються підстановкою у неї значень та , а інтервальні – за формулою: , де =. За розрахунками ; С(1)=1,365; С(2)=1,855.
Інтервальні оцінки прогнозів дорівнюють: та .
Оцінки параметрів моделі Брауна Таблиця 3.3.6
| 0 | 49638,7 | 49638,7 | 0,00 | ||
| 1 | 49755 | 49764,77 | 126,1105 | 49890,88 | -135,88 |
| 2 | 49929,3 | 49767,23 | 59,5293 | 49826,76 | 102,5415 |
| 3 | 50000 | 49920,07 | 109,7746 | 50029,85 | -29,8459 |
| 4 | 50100 | 50002,69 | 95,15014 | 50097,84 | 2,163725 |
| 5 | 50300 | 50099,81 | 96,21037 | 50196,02 | 103,9844 |
| 6 | 50926 | 50290,64 | 147,1627 | 50437,8 | 488,1959 |
| 7 | 50840 | 50882,06 | 386,3787 | 51268,44 | -428,441 |
| 8 | 51298,7 | 50878,56 | 176,4426 | 51055 | 243,6977 |
| 9 | 51475,2 | 51276,77 | 295,8545 | 51572,62 | -97,4217 |
| 10 | 51616,6 | 51483,97 | 248,1178 | 51732,09 | -115,486 |
| 11 | 51707 | 51626,99 | 191,5298 | 51818,52 | -111,524 |
| 12 | 51800 | 51717,04 | 136,8833 | 51853,92 | -53,9204 |
| 13 | 51944 | 51804,85 | 110,4623 | 51915,32 | 28,68488 |
| 14 | 52100 | 51941,42 | 124,5179 | 52065,94 | 34,06376 |
| 15 | 52200 | 52096,93 | 141,2091 | 52238,14 | -38,1434 |
| 16 | 52100 | 52203,43 | 122,5189 | 52325,95 | -225,952 |
| 17 | 51700 | 52120,34 | 11,8025 | 52132,14 | -432,138 |
| 18 | 51300 | 51738,89 | -199,945 | 51538,95 | -238,947 |
| 19 | 50499,9 | 51321,51 | -317,029 | 51004,48 | -504,576 |
| 20 | 50105,6 | 50545,31 | -564,272 | 49981,04 | 124,5597 |
| 21 | 49710,8 | 50094,39 | -503,237 | 49591,15 | 119,6477 |
| 22 | 49291,8 | 49700,03 | -444,61 | 49255,42 | 36,37822 |
| 23 | 48415,5 | 49288,53 | -426,785 | 48861,74 | -446,241 |
| 24 | 48202,5 | 48455,66 | -645,443 | 47810,22 | 392,2811 |
| 25 | 47810,22 | ||||
| 26 | 47164,78 |
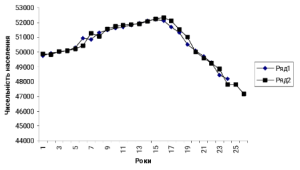
Рис.3.3.3. Результати згладжування та прогнозування за адаптивною моделлю Брауна.
На рис.3.3.3 показані результати згладжування і прогнозування за побудованою моделлю. Ряд 1 відповідає фактичним даним, ряд 2 – розрахованим за моделлю Брауна, при цьому вказані точкові прогнози на два роки вперед. ►
Метод Хольта. Адаптивна модель за методом Хольта представляє динамічний процес у вигляді лінійно-адитивного тренду:
(3.3.22)
де – прогнозована оцінка рівня ряду , яка розраховується в момент часу на кроків вперед,
– оцінка поточного (-го) рівня часового ряду,
– оцінка поточного приросту.
Припускається, що випадкові залишки е мають нормальний закон розподілу з нульовим математичним сподіванням та дисперсією .
У цьому методі послаблені умови однопараметричності моделі Брауна за рахунок введення двох параметрів згладжування – та , ().
Коефіцієнти лінійної моделі (3.3.34) методом Хольта розраховуються за такими співвідношеннями:
, (3.3.23)
, (3.3.24)
де еt – похибка прогнозу рівня обчислена в момент часу (t-1) на один крок вперед, .
Коефіцієнт має значення, близьке до останнього рівня, і представляє закономірну складову цього рівня; коефіцієнт – визначає приріст, що склався наприкінці періоду спостережень, але характеризує також швидкість зростання показника на більш ранніх етапах. Початкові значення параметрів моделі знаходяться за методом найменших квадратів на основі декількох перших спостережень. Оптимальні значення параметрів згладжування та визначаються методом багатовимірної числової оптимізації і являються сталими для усього періоду спостереження.
Після оцінювання параметрів та прогноз на τ моментів часу, тобто , розраховується як сума оцінки середнього поточного значення () та очікуваного показника зростання (), помноженого на період випередження τ, тобто
=+τ. (3.3.25)
За допомогою оператора L можна зрушити усю послідовність даних на один крок назад: . Застосування оператора до спостережень і коефіцієнтів моделі Хольта дозволяє представити її як модель у вигляді:
. (3.3.26)
Формулювання адаптивних моделей в термінах лінійних параметричних моделей ARMA (авторегресії – ковзної середньої) – дозволяє теж тлумачити їх як підмножину класу лінійних параметричних моделей. Отже, встановлюється відповідність між двома різними підходами до моделювання часових рядів.
Метод еволюції для двох- і трьохпараметричних моделей. Підбір параметрів адаптації є вузьким місцем для усіх адаптивних методів, основаних на експоненціальному згладжуванні. Як правило, для кожного набору значень параметрів розраховують серію прогнозів за даним методом згладжування і порівнюючи одержані середньоквадратичні похибки прогнозів обирають кращі з них. Звичайно уся громіздкість процедури перекладається на комп’ютер.
Альтернативу базовим моделям складає динамічне коригування параметрів згладжування. В методах еволюції і симплекс-планування параметри адаптації постійно змінюються на кожному кроці . Для кожного параметра згладжування задається декілька значень. Кожний набір параметрів згладжування розглядається як одна точка. Центральна точка вважається прогнозною, а інші – контрольними. Згідно з алгоритмом методу для наступного кроку кращим набором вважаються ті значення, для яких на попередньому кроці була побудована точніша модель. Методи еволюції відрізняються від симплекс-планування лише геометричною фігурою, яка відображає сполучення параметрів згладжування (квадрат, куб, тетраедр тощо). Значення параметрів, що спочатку є довільними, постійно змінюються, і алгоритм їх зміни направлений на якнайшвидше вилучення помилок прогнозування.
Для забезпечення адаптації параметра згладжування однопараметричної моделі до зміни динаміки ряду можна, використовуючи три різних параметри, які називаються відповідно нормальним (α), низьким () і високим (), отримати не одну, а три оцінки наступного рівня ряду. При цьому оцінка, отримана за нормальним значенням параметра, вважається прогнозом, а інші дві оцінки являються контрольними величинами.
Після одержання нового фактичного рівня ряду визначають величину параметра, яка дає найменшу абсолютну або згладжену похибку і, отже, є найкращою для попереднього і поточного кроків. Припускається, що параметр буде найкращим і на поточному кроці прогнозування. Дане значення вважається нормальним, і вже від нього розраховуються нові низьке і високе значення (), які повинні знаходитися в певному інтервалі (,).
Отже, значення параметру згладжування, яке обирається спочатку навмання, постійно змінюється у напрямку компенсації і усування постійно виникаючих похибок прогнозування.
Таблиця 3.3.5
Основні формули для прогнозування за адаптивним методом Брауна
| Вид моделі і відповідна їй експоненціальна середня | Початкові
умови |
Оцінки коефіцієнтів | Оцінка прогнозу | для границь інтервалу надійності |
| ; | ||||
| ; | ||||