7.1. Критерії визначення якісного прогнозу. Якість прогнозу характеризують такі поширені в прогностичній літературі терміни, як точність і надійність. Проте зміст цих термінів часто тлумачиться достатньо неоднозначно. Це можна пояснити тим, що на сьогоднішній день не знайдено ефективного підходу до оцінки якості прогнозу, окрім його практичного підтвердження.
Про точність прогнозу прийнято судити по розміру помилки прогнозу – різниці між прогнозним і фактичним значенням досліджуваного показника. Проте такий підхід до оцінки точності прогнозу можливий тільки, якщо дослідник має інформацію про справжні значення часового ряду, який він оцінював у ході розробки прогнозів. Наприклад, період випередження вже закінчився, і дослідник має фактичні значення змінної (це можливо при короткостроковому прогнозуванні) або, прогноз знаходиться в стадії розробки, тобто прогнозування здійснюється для деякого моменту часу в минулому, для котрого існують фактичні дані. Спрощена схема періодів прогнозування показана на рис. 7.1.
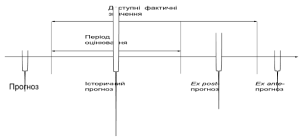
Рис. 7.1. Спрощена схема періодів прогнозування.
У останньому випадку мова йде про використання ex post-прогнозу. Його суть полягає у побудові моделі за меншим обсягом даних () із наступним порівнянням прогнозних оцінок за останніми точками (для від до ) з відомими фактичними, але спеціально залишеними рівнями ряду. Отримані ретроспективно помилки прогнозу якоюсь мірою характеризують точність застосовуваної методики прогнозування і можуть виявитися корисними при зіставленні декількох прогнозів.
Параметричні методи аналізу точності прогнозів. За результатами ex post-прогнозу розраховуються наступні показники точності прогнозів за кроків:
Середня квадратична похибка:
, (7.1.1)
корінь із середньоквадратичної похибки
, (7.1.2)
середня абсолютна похибка:
(7.1.3)
корінь з середньоквадратичної похибки у відсотках:
, (7.1.4)
середня абсолютна похибка у відсотках (МАРЕ):
МАРЕ=, (7.1.5)
Чим менше значення цих величин, тим вища якість ретропрогнозу. На практиці ці характеристики використовуються досить часто. Даний підхід дає гарні результати, якщо на періоді ретропрогнозу не містяться принципово нові закономірності. На основі останніх двох критеріїв можна робити висновок про деякий загальний рівень адекватності моделі на основі їх порівняння. Цей рівень наведений у таблиці:
| MAPE, RMSE | Точність прогнозу |
| Менше 10% | Висока |
| 10% – 20% | Добра |
| 20% – 40% | Задовільна |
| 40% – 50% | Погана |
| Більше 50% | Незадовільна |
Вадою обговорених вище характеристик точності прогнозів є їх залежність від обраних одиниць виміру. Було б корисним вказати безрозмірний показник, аналогічний до коефіцієнта кореляції. Одним з таких показників є коефіцієнт невідповідності Тейла, чисельником якого є середньоквадратична похибка прогнозу, а знаменник дорівнює квадратному кореню із середнього квадрата фактичних значень:
=. (7.1.6)
Перевага коефіцієнта Тейла полягає у тому, що його значення завжди знаходяться в межах від нуля до одиниці. Якщо всі прогнози абсолютно точні, то =0. Якщо всі прогнози дорівнюють нулю, а жодне з фактичних значень не дорівнює нулю або навпаки, дорівнюватиме одиниці. Таким чином, маленьке значення вказує на те, що прогноз є точним, але максимального значення не існує. Значення, яке дорівнює одиниці, відповідає ситуації, коли всі прогнозні значення дорівнюють нулю, що нереально при прогнозуванні номінальних величин, але при розгляді змін такий прогноз відповідає моделі “без змін”. Більші за одиницю значення вказують на те, що прогноз гірший, ніж прогноз “без змін”.
Коефіцієнт невідповідності Тейла () може бути розкладений на три частини:
пропорцію зсунення =, (7.1.7)
пропорцію дисперсії = , (7.1.8)
пропорцію коваріації = . (7.1.9)
Зазначимо, що ++=1. Критерій зсуву пропорції () використовується, щоб перевірити, чи є систематичне відхилення середніх розрахованих (fitted) та фактичних рядів, тобто чи дає модель систематично завищені або занижені прогнози. Чим менше значення , тим краще. Якщо дорівнює нулю, у розрахованих (прогнозних) значеннях немає зсунень, тобто з моделлю все гаразд. Пропорція дисперсії () використовується, щоб переконатися, що модель має достатні динамічні властивості для відтворення дисперсії фактичних рядів. Наприклад, модель може відтворювати систематично менші коливання, ніж фактичні. Як і у випадку критерію , менше значення вказує на менше зсунення. Пропорція коваріації вказує, як корелюють фактичні та розраховані ряди. Якщо дорівнює 1, то фактичні та розраховані ряди корелюють ідеально.
Критичні точки важливі як критерії якості, оскільки деякі моделі можуть бути точними, але погано передбачати зміни тенденції (наприклад, поворотні точки в циклах), тобто погано відтворювати критичні точки. Інші моделі можуть бути неточними, але мати гарний динамічний характер. Загалом може бути певний компроміс між точністю та динамічними властивостями моделі. Формального тесту для оцінки цієї властивості не існує. Проте візуальний огляд розрахованих та фактичних рядів звичайно одразу виявляє, добре модель відтворювати критичні точки чи ні.
Обговорені характеристики точності прогнозів є параметричними у тому сенсі, що вони потребують виконання заданих припущень відносно властивостей математичного сподівання та дисперсії, які чинні за умов нормальності відповідних розподілів. Наприклад, використовуючи MSE, ми неявно припускаємо, що всі похибки прогнозу мають однакові і постійні математичні сподівання та дисперсії. В реальних економічних ситуаціях найчастіше порушуються припущення гомоскедастичності та відсутності автокореляції. Можна стверджувати, що кожного разу прогноз будується у новій ситуації, отже, порівняння числової точності прогнозів, зроблених у різні моменти часу, не зовсім коректне. Наведені міркування призвели до використання непараметричних методів аналізу точності прогнозів.
Непараметричні методи аналізу точності прогнозів. Непараметричні методи не залежать від вигляду розподілу, і отже не потребують припущення про нормальність розподілів. Це особливо корисно, коли йдеться про дані, які не дозволяють використовувати числові шкали. Розглянемо два типи непараметричних критеріїв: критерій знаків та рангові критерії.
К р и т е р і й з н а к і в для порівняння точності двох послідовностей прогнозів базується на відсотку випадків, коли метод визначення прогнозу А краще, ніж метод В. Таке порівняння проводиться для індивідуальних прогнозів однакових подій (змінних). Якщо обидва методи дають однакову точність, ймовірність відповіді “так” на запитання “чи прогноз А кращий за прогноз Б” складає 0,5 для кожного з випадків прогнозування. Число К випадків, коли прогноз А кращий, підпорядковано біноміальному розподілу ймовірностей
. (7.1.10)
Отже, можна підрахувати імовірність того, що К ≥ х. Якщо довжина послідовності прогнозів значна, для оцінки імовірностей можна використати нормальну апроксимацію біноміального розподілу.
Критерій знаків можна також використовувати для перевірки значущості описової статистики, відомої під назвою “відсоток кращих результатів”, яка показує відсоток випадків, у яких один метод прогнозування кращий за інший і розраховується за формулою:
, (7.1.11)
де – кількість прогнозів, підтверджених фактичними даними;
– кількість прогнозів, не підтверджених фактичними даними. Коли всі прогнози підтверджуються, =0 і =1, якщо ж усі прогнози не підтвердилися, то , а отже і дорівнюють 0.
Р а н г о в і к р и т е р і ї. При застосуванні цих критеріїв чисельна характеристика точності (абсолютна похибка, коли маємо один прогноз, або MSE, коли розглядається послідовність прогнозів) замінюється рангами, які потім перевіряються на значущість. Наприклад, якщо послідовності прогнозів показників А та В одержуються за допомогою k методів, то спочатку обчислюються MSE, потім їх значення ранжуються від 1 (найменша MSE) до k (найбільша MSE) (відповідні ранги позначаються через ra, та rb, для і =). Після знаходження різниць (dі) між рангами обчислюють коефіцієнт рангової кореляції Спірмена
rs=1 -. (7.1.12)
За нульову гіпотезу приймається відсутність залежності між рангами, тобто жоден з методів не є гіршим за решту. Гіпотеза відкидається, коли значення rs досить велике.
Хоча непараметричні методи мають свої переваги, важливо усвідомлювати, що вони ігнорують частину доступної інформації. Так, критерії знаків та рангів не враховують числові значення похибок.
Розмір помилки ретроспективного прогнозу не можна розглядати як остаточний доказ придатності, або навпаки, непридатності застосовуваного методу прогнозування. До неї варто ставитися з відомою обережністю і при її застосуванні в якості міри точності необхідно враховувати, що вона отримана при використанні лише частини наявних даних. Проте ця міра точності має більшу наочність і теоретично більш надійна, ніж похибка прогнозу, обчислена для періоду характеристики котрого вже були використані при оцінюванні параметрів моделі.
Перевірка гіпотези про правильність вибору виду тренду. В практичній роботі проблему точності прогнозу треба вирішувати, як правило, тоді, коли період випередження щ е не пройшов, і справжнє значення прогнозованої змінної не відоме. У цьому випадку проблема точності може розглядатися з точки зору зіставлення апріорних якостей, властивостей прогностичних моделей. По суті мова йде про статистичний аналіз залишків, тобто відхилень від тренду. Досліджування залишкової компоненти робиться з метою перевірки гіпотез: чи правильно підібраний тренд; чи представляє залишкова послідовність стаціонарний випадковий процес. У випадку підтвердження цих гіпотез прогноз може бути зроблений за обома складовими часового ряду: за трендом – шляхом простої екстраполяції, за відхиленнями від тренду – за допомогою існуючих методів прогнозування стаціонарних випадкових процесів. Підсумок двох одержаних таким чином прогнозів дає загальний прогноз показника.
При правильному виборі виду тренду відхилення від нього будуть мати випадковий характер. Це означає, що зміна випадкової величини не залежить від фактора часу.
Найбільш простим способом перевірки припущення про випадковість є визначення коефіцієнту кореляції між відхиленнями від тренду і чинником часу та перевірка його значущості. Однак цей зв’язок може бути нелінійним. Тому характер відхилень доцільно вивчати за допомогою непараметричних критеріїв, таких як, заснований на медіані вибірки, критерій “зростаючих” та “спадаючих” серій тощо. Позначимо розходження між фактичними і розрахованими за моделлю рівнями часового ряду(t=1,2,…,п).
К р и т е р і й с е р і й, о с н о в а н и й н а м е д і а н і в и б і р к и. Згідно з критерієм серій ряд з величин розташовують у порядку зростання їх значень і знаходять медіану одержаного варіаційного ряду, тобто значення, що знаходиться в середині для непарного п або середню арифметичну з двох середніх значень для п парного. Повертаючись до вхідної послідовності і порівнюючи значення цієї послідовності з , ставлять знак «плюс», якщо значення , перевищує медіану, і знак «мінус», якщо воно менше за медіану; у випадку однаковості порівнюваних величин відповідне значення пропускається. Отже, одержується послідовність, яка складається із плюсів та мінусів, загальна кількість яких не перевищує п. Послідовність поспіль розташованих плюсів або мінусів називається серією. Для того щоб послідовність була випадковою вибіркою, довжина найдовшої серії не повинна бути занадто великою, а загальна кількість серій – занадто малою.
Позначимо довжину найдовшої серії через Кmax, а загальну кількість серій – через v. Вибірка вважається випадковою, якщо виконуються наступні нерівності для 5% -го рівня значущості:
, (7.1.13)
v>,
де квадратні дужки означають цілу частину числа.
Якщо хоча б одна з цих нерівностей порушується, то гіпотеза про випадковий характер відхилень рівнів часового ряду від тренду спростовується і, отже, модель тренду признається неадекватною.
Перевірка гіпотези про нормальний закон розподілу випадкової компоненти. У деяких випадках, наприклад при визначенні похибки прогнозу за авторегресійними моделями, необхідно перевірити гіпотезу про те, що відхилення від тренду або від певної моделі відповідають закону нормального розподілу. Оскільки часові ряди соціально-економічних процесів, як правило, не дуже довгі, то перевірка розподілу на нормальність може бути зроблена лише наближено за допомогою дослідження показників асиметрії (А) і ексцесу (Е). Для нормального розподілу асиметрія і ексцес певної генеральної сукупності дорівнюють нулю. Ми припускаємо, що відхилення від тренду представляють собою вибірку з генеральної сукупності, тому можна визначити тільки вибіркові характеристики асиметрії й ексцесу та їх похибки:
; ; (7.1.14)
; . (7.1.15)
У цих формулах – вибіркова характеристика асиметрії; – вибіркова характеристика ексцесу; – середньоквадратична похибка вибіркової характеристики асиметрії; – середньоквадратична похибка вибіркової характеристики ексцесу.
Якщо одночасно виконуються наступні нерівності:
; , (7.1.16)
то гіпотеза про нормальний характер розподілу випадкової компоненти не відхиляється.
Якщо виконується хоча б одна з нерівністей
; , (7.1.17)
то гіпотеза про нормальний характер розподілу відхиляється, модель тренду признається неадекватною. Інші випадки потребують додаткової перевірки за допомогою більш складних критеріїв. Для адекватних моделей доцільно ставити питання про оцінювання їх точності. Вважається, що моделі з меншим розходженням між фактичними і розрахунковими значеннями краще відображають досліджуваний процес у майбутньому. Для характеристики ступеня близькості використовуються наступні описові статистики:
середнє квадратичне відхилення (або дисперсія)
; (7.1.18)
середня відносна похибка апроксимації (чим ближче до 0, тим точніша модель)
; (7.1.19)
коефіцієнт сходження
, (7.1.20)
коефіцієнт детермінації (чим ближче до 1, тим точніша модель)
. (7.1.21)
У наведених формулах (7.1.18-7.1.21) – кількість рівнів ряду, – кількість пояснюючих змінних в моделі, – оцінки рівнів ряду за моделлю, – середнє арифметичне значення вибірки.
На основі розглянутих показників можна зробити вибір з декількох адекватних моделей найбільш точної. Помилка прогнозу, обчислена для періоду, характеристики котрого вже були використані при оцінюванні параметрів моделі, як правило, будуть незначними і мало залежатимуть від теоретичної обґрунтованості, застосованої для побудови моделі.
Оскільки формально-статистичний вибір кращої моделі у багатьох випадках не дає повної впевненості у його правильності: гарний прогноз може бути отриманий і по поганій моделі, і навпаки, то, про якість прогнозів застосовуваних методик і моделей можна судити лише по сукупності зіставлень прогнозів і їхньої реалізації. При цьому незалежно від обраної методики ат моделі прогнозування джерелами помилок прогнозу можуть бути:
- природа змінних (випадковий характер змінних гарантує, що прогноз буде відхилятися від справжніх величин, навіть якщо модель правильно специфікована та її параметри точно відомі);
- природа моделі (сам процес оцінювання спричиняє похибки оцінок параметрів);
- помилки, що вносяться прогнозом незалежних випадкових величин (пояснюючих змінних);
4) помилки специфікації моделі.
Інтегровані критерії точності й адекватності. Схема формування інтегрованих критеріїв точності, а також загального критерію якості прогнозування полягає у тому, що формується склад окремих критеріїв, на основі яких розраховується інтегрований показник (так, точність можна характеризувати тільки коефіцієнтом детермінації, або дисперсією і середньою помилкою апроксимації, або усіма трьома переліченими критеріями).
Попередньо для кожного окремого критерію розробляється процедура його нормування. Нормований критерій одержується із вихідної статистики критерію таким чином, щоб виконувалися умови: нормований критерій дорівнює 100, якщо модель абсолютно точна (адекватна), нормований критерій дорівнює 0, якщо модель абсолютно неточна (неадекватна).
Узагальнений критерій якості моделі розраховується як зважена сума узагальненого критерію точності (його вага 0,75) і узагальненого критерію адекватності (його вага 0,25), тобто точності надається перевага. За характеристику точності обирається нормоване значення середньої відносної похибки апроксимації, а за критерій адекватності — нормоване значення критерію Дарбіна—Уотсона і характеристики нормального закону розподілу залишкової компоненти. Числове значення узагальненого критерія якості знаходиться в діапазоні від 0 до 100 (мінімум відповідає абсолютно поганій моделі, а максимум – моделі, що ідеально відображає розвиток показника). Досвід застосування цього показника свідчить про надійність моделей, оцінка якості яких не менша за 75.
Вище наведені міри якості прогнозу виходять із незначного його відхилення від фактичних значень, але зрозуміло, що деякі змінні прогнозувати простіше, ніж інші. Так вважається, що обсяг поточного рахунку платіжного балансу, який визначається як різниця двох великомасштабних показників – імпорту та експорту, прогнозувати важче, ніж величини, які змінюються відносно повільно, наприклад, тривалість життя, рівень безробіття. Отже, для визначення оптимального прогнозу необхідний системний критерій. Точно кажучи, оптимальний прогноз слід визначати з розгляду функції витрат користувача прогнозу, тобто з аналізу збитків через помилку прогнозу, а також з порівняння додаткового виграшу від зменшення помилки та витрат на удосконалення прогнозу. Отже, оптимальним вважається найкращий прогноз, який можна одержати за наявних обставин.
Оптимальний прогноз – це зроблене на основі економічної теорії передбачення, яке використовує всю доступну на момент побудови прогнозу інформацію. Для оптимального прогнозу граничний виграш та граничні витрати співпадають.
Оптимальний прогноз ще отримав назву прогноз раціональних сподівань. Раціональні сподівання можуть відрізнятись від фактичних значень, але будь-яка різниця повинна бути випадковою та не передбачуваною. Оскільки раціональні сподівання основуються на коректній економічній теорії, вони мають властивості незсуненості (за умови квадратичної функції витрат) та ефективності.
Незсуненість означає, що помилка прогнозу має нульове математичне сподівання.
Ефективність передбачає, що в процесі прогнозування буде використана вся доступна інформація, отже помилка прогнозу не буде корелювати із цією інформацією.
Існують численні критерії перевірки того, чи є послідовність прогнозів раціональною [16]. Стандартний критерій незсуненості потребує перевірки гіпотези, що та водночас, для наступної моделі:
, (7.1.22)
де – ряд фактичних значень або спостережень;
– ряд прогнозованих значень;
– випадкові залишки.
Перевірка ефективності є більш складною, оскільки неможливо коректно визначити відповідний масив інформації, відносно якого похибки прогнозу будуть не корельованими.
Узагальнюючи огляд критеріїв визначення якісного прогнозу, можна зробити висновок, що потрібно користуватися системою критеріїв, які повинні враховувати:
- кількість зусиль, що витрачаються на побудову моделі і наявність готових комп’ютерних програм;
- швидкість, із якою метод уловлює істотні зміни у поведінці ряду, наприклад, раптовий зсув математичного сподівання або збільшення кута нахилу лінії тренду;
- існування серійної кореляції у помилках;
- незмінюваність первинних даних;
- повний обсяг роботи у деяких сферах діяльності – тисячі рядів щомісяця потребують оновлення, невеликі витрати і швидкість мають першорядне значення;
- терміновість прогнозування.
7.2. Побудова комбінованого прогнозу.
Формулювання проблеми. Серед дослідників немає одностайної думки щодо існування найкращого методу прогнозування. Досвід застосування різноманітних підходів до прогнозування показує, що кожний метод призводить до різних результатів. Отже, як правило, виходить декілька відмінних прогнозів того ж самого економічного показника. Постає питання: чи переважає якийсь метод решту, і чи можливо якимось чином скомбінувати прогнози, одержані різними методами, і побудувати узагальнений прогноз, який буде точніший за індивідуальні?
Можна сподіватися, що будь-який прогноз, відкинутий через його не оптимальність, майже завжди містить певну корисну незалежну інформацію. Така інформація може бути двосторонньою: по-перше, кожний прогноз оснований на інформації, яка є спеціальною для даного підходу, і тому не враховується в інших методах; по-друге, кожний прогноз відтворює певну форму взаємозв’язків між змінними, що відрізняється від зв’язків, досліджуваних в інших моделях. Об’єднання незалежно одержаних прогнозів залучає обидва види додаткової інформації і, якщо припустити, що кожна з моделей описує лише один бік динаміки заданого процесу, то спільне використання декількох моделей дозволяє точніше і повніше описати й спрогнозувати цю динаміку. Не випадково сучасна теорія систем пропонує стратифікований підхід до опису складних систем. Така точка зору привела до ідеї об’єднання прогнозів і формуванні на цій основі комбінованого або об’єднаного прогнозу.
Об’єднання може здійснюватися як на основі прогнозів, одержаних з різних джерел, наприклад експертним шляхом і за допомогою моделей, так і за прогнозами, побудованими за допомогою статистичних моделей одного класу.
Спосіб об’єднання окремих прогнозів, як правило, полягає у тому, щоб представити комбінований прогноз у вигляді зваженої суми окремих прогнозів:
=, (7.2.1)
де – і-й окремий прогноз, одержаний для моменту часу ;
М – кількість об’єднуваних прогнозів;
– вагові коефіцієнти окремих прогнозів;
Сума усіх вагових коефіцієнтів повинна давати одиницю, і окремі ваги знаходяться в інтервалі [0,1]. Очевидно, що основна проблема, яка при цьому виникає, – визначення ваг , оскільки саме вони будуть визначати якість об’єднаного прогнозу. На практиці завжди прагнуть надати більшу вагу тому набору прогнозів, який містить менші за величиною середньоквадратичні похибки. Існує багато способів визначення вагових коефіцієнтів, найбільш відомими серед яких є два:
- дисперсійно-коваріаційний метод, що дозволяє зводити декілька незміщених прогнозів в лінійну комбінацію з найменшою дисперсією, ваги якої залежать від дисперсій та коваріацій похибок прогнозів;
- регресійний метод, який є узагальненням дисперсійно-коваріаційного на випадок зсунення прогнозів.
Спосіб комбінування прогнозів, одержаних за статистичними моделями одного класу, породжує ряд питань. Наприклад, які прогнози можуть об’єднуватися, якою повинна бути кількість прогнозів, якою повинна бути процедура об’єднання тощо. Об’єднання прогнозів пов’язано із такими ускладненнями, як корельованість прогнозів, одержаних за різними моделями, наявність змін властивостей похибок прогнозу із часом, зміщення комбінованого прогнозу тощо. Кожне з названих ускладнень потребує застосування спеціального підходу. Поки не розроблено широко уживаних правил, суб’єктивні судження дослідника є складовою частиною прийняття рішення про те, як комбінувати прогнози.
Дисперсійно-коваріаційний метод. Об’єднання прогнозів розглянемо на прикладі побудови середньозваженого прогнозу двох окремих прогнозів, оскільки розповсюдження одержаних результатів на більшу кількість окремих прогнозів здійснюється досить просто. У загальному випадку два не зсунені прогнози можна скомбінувати для одержання нового прогнозу. Будемо виходити з мінімізації дисперсії похибки прогнозу, тобто використовуючи квадратичну функцію збитків.
Нехай маємо на період два не зсунені прогнози і , дисперсії яких та і коваріація . Новий незміщений прогноз будується за правилом
. (7.2.2)
Дисперсія похибки комбінованого прогнозу буде дорівнювати
. (7.2.3)
Мінімізуючи цей вираз по , одержимо, що
, (7.2.4)
Отже, ваги у оптимальній лінійній комбінації залежать від дисперсій та коваріацій похибок прогнозу, звідки походить назва “дисперсійно-коваріаційний метод”.
Кореляція між похибками окремих прогнозів дорівнює і підстановка замість та у (7.2.3) дає
. (7.2.5)
Звідси можна показати, що та і тому менше або дорівнює мінімальному з та . Отже, комбінований прогноз принаймні такий же точний, як кращий з двох прогнозів, які взято компонентами.
Оптимальна величина не може бути одержана на початковій стадії синтезу прогнозу, оскільки вона змінюється із накопиченням знань про відносну ефективність двох окремих прогнозів. Більш того, на попередній стадії ще невідомі ні дисперсії похибок окремих прогнозів , ні коефіцієнти кореляції між цими похибками. Їх треба оцінювати. Узагальнення цього методу до комбінування прогнозів відбувається за формулою
, (7.2.6)
де – коваріаційна матриця похибок прогнозу розмірності ;
– -мірний вектор-стовпчик, усі координати якого є одиницями.
Аналіз знайдених оптимальних ваг дозволяє зробити наступні висновки:
- по-перше, очевидно, що інтуїтивно приваблива думка простого вибору найкращого (з найменшою дисперсією похибки) прогнозу і його використання здається сумнівною тому, що у загальному випадку комбінований прогноз має меншу дисперсію похибки.
- по-друге, якщо та дорівнюють один одному, то у (5.2.9) ваги також рівні і комбінований прогноз є простим середнім значенням компонентів.
- по-третє, якщо коваріація похибок прогнозів додатна і більша за одну з дисперсій (наприклад, якщо від’ємне), один із ваг буде від’ємним, а інший перевищуватиме одиницю. Зауважимо, що від’ємність ваги не обов’язково означає, що прогноз є поганим.
- по-четверте, коли дисперсія похибки прогнозу прямує до нуля, вага цього прогнозу прямує до одиниці. Отже, чим надійніший прогноз, тим більшу вагу він має.
Регресійний метод є узагальненням дисперсійно-коваріаційного методу. Його можна тлумачити як оцінювання параметрів регресійного рівняння виду
, (7.2.7)
де збурення v має нульове середнє.
Новий комбінований прогноз є лінійною комбінацією М прогнозів. Коефіцієнти , оцінюються за методом найменших квадратів. Якщо усі прогнози є незміщеними, то доданок можна опустити. У цьому випадку оцінки коефіцієнтів будуть співпадати із оцінками вектора попереднього методу.