1. Основні поняття та попередній аналіз часових рядів

Сучасні дослідження макроекономічної динаміки, процесів перехідної економіки, фінансових ринків спираються на аналіз взаємозв’язків соціально-економічних даних, що подаються у вигляді часових рядів. Врахування часової структури даних про реальні економічні процеси дозволяє адекватно відобразити їх в економетричних моделях. Усвідомлення цього факту призвело як до  ревізії багатьох макроекономічних теорій, так і до бурхливого розвитку специфічних методів аналізу таких даних. Інформаційне представлення динаміки розвитку соціально-економічних процесів, коригування рівнів ЧР, декомпозиція ЧР, . Знання цих методів та способів застосування їх до прогнозування соціально-економічних процесів є необхідною складовою підготовки економістів-дослідників (аналітиків).

1.1. Інформаційне представлення динаміки розвитку соціально-економічних процесів

Соціально-економічні процеси найчастіше спостерігаються у вигляді ряду послідовних, розташованих у хронологічному порядку значень того чи того показника. 

Динамічний ряд – це сукупність спостережень одного показника, впорядкованих залежно від значень іншого показника, що послідовно зростають або спадають.

Часовий  ряд – це ряд динаміки, впорядкований за часом, або сукупність спостережень економічної величини у різні моменти часу. 

Теоретично вимірювання можна реєструвати безперервно, але зазвичай їх здійснюють через однакові проміжки часу, тобто дискретно, і нумерують за елементами вибірки. Складовими ряду спостережень є числові значення показника, які називаються рівнями ряду, та моменти або інтервали часу, до яких належать рівні. Часовий ряд (ЧР) можна записати у стислому вигляді: , ,  де – рівновіддалені моменти спостережень (година, доба, місяць, квартал, рік тощо). Під довжиною часового ряду розуміють час, що минув від першого до останнього моменту спостереження. Часто довжиною ряду називають кількість рівнів n, які утворюють часовий ряд.

Залежно від характеру досліджуваних соціально-економічних показників часові ряди поділяють на моментальні, інтервальні та похідні.

Часові ряди, утворені показниками, що характеризують економічне явище на певні моменти часу, називають моментальними; прикладом такого ряду є дані щодо розміру виданих позичок відділенням Держбанку (табл.1.1.1).

Таблиця 1.1.1

Моментальний часовий ряд

Дата надання позички	01.10.	05.10.	12.10.	23.10.	03.11.	07.11.
Розмір наданої позички, тис. грош. од.	3747	3710	3839	3783	3747	3710

Якщо рівні часового ряду утворюються шляхом агрегування за певний проміжок (інтервал) часу, такі ряди називають інтервальними часовими рядами; приклад наведено в табл. 1.1.2.

Таблиця 1.1.2

Інтервальний часовий ряд

Місяць	Січень	Лютий	Березень	Квітень	Травень
Валовий внутрішній продукт, млн грн	6578	7016	7353	7353	7941

Часові ряди можуть бути створені як із абсолютних значень економічних показників, так і з середніх або відносних величин – це похідні ряди; приклад такого ряду наведено в табл. 1.1.3.

Таблиця 1.1.3

Часовий ряд, утворений із середніх значень показника

Місяць	Січень	Лютий	Березень	Квітень	Травень
Середня зарплата загалом, грн/міс.	152,2	153,7	165,8	161,6	163,71

Основні характеристики динаміки розвитку соціально-економічних процесів. Для аналізу соціально-економічних показників абсолютні рівні моментальних або інтервальних часових рядів, а також рівні середніх величин часто доводиться перетворювати на відносні величини. Найпоширеніші характеристики динаміки розвитку соціально-економічних процесів та їхні розрахунки наведено  в табл. 1.1.4.

 Таблиця  1.1.4

Характеристики динаміки часового ряду

Характеристики	Розрахункові формули
1	2
1. Абсолютний приріст
2. Коефіцієнт зростання
3. Коефіцієнт приросту
4. Темп зростання
5. Темп приросту	= -100%, або
6. Середня арифметична
7. Середня хронологічна
8. Середній абсолютний приріст
9. Середній темп зростання
10. Середній темп приросту

Для визначення змін, що відбуваються з досліджуваним явищем, передусім обчислюють швидкість розвитку цього явища за часом. Показником швидкості слугує абсолютний приріст, який характеризує величину зміни показника за інтервал часу між порівнюваними періодами й обчислюється за формулою:

                                               ,                                                                            (1.1.1)

де – і-й рівень часового ряду ();

– індекс початкового рівня; і може бути обраний будь-яким залежно від мети дослідження: за отримують ланцюгові показники, за отримують базові показники  із базовим початковим рівнем ряду тощо.

Точніше, швидкість зміни показника характеризує приріст за одиницю часу; ця величина має назву середнього абсолютного приросту:

.                                                                        (1.1.2)

Зокрема, середній абсолютний приріст за весь період спостереження для заданого часового ряду дорівнює:

(1.1.3)

і характеризує середню швидкість зміни часового ряду, де – індекс останнього спостереження.

Для визначення відносної швидкості зміни економічного явища як одиницю часу використовують відносні показники: коефіцієнти зростання і приросту (якщо ці показники виражені у відсотках, їх називають відповідно темпами зростання і приросту). Зазначимо, що в усіх наступних формулах індекс початкового рівня, стосовно якого здійснюють порівняння, також визначають за допомогою індексу k, як і раніше для показника абсолютного приросту.

Коефіцієнт зростання для і-го періоду обчислюють за формулою:

,                                                                          (1.1.4)

, якщо рівень підвищується; , якщо рівень зменшується; за рівень не змінюється.

Коефіцієнт приросту дорівнює

=     або                                                                       (1.1.5)

На практиці часто застосовують показники темпу зростання і темпу приросту:

,                                                                (1.1.6)

де − темп зростання для і-го періоду;

=   або  ,                            (1.1.7)

де − темп приросту для і-го періоду. Темп приросту показує, на скільки відсотків рівень одного періоду збільшився стосовно рівня іншого періоду, тобто цей показник характеризує відносну величину приросту у відсотках.

Порівняння абсолютного приросту і темпу приросту за той самий інтервал часу показує, що в реальних економічних процесах уповільнення темпу приросту часто не супроводжується зменшенням абсолютних приростів.

Абсолютне значення одного відсотка приросту визначають як відношення абсолютного приросту до темпу приросту у відсотках .

Середню швидкість зміни показника, що вивчається, за певний період характеризує також середній темп зростання. Його розраховують за формулою середньої геометричної:

,                          (1.1.8)

де − середні темпи зростання за окремі інтервали часу.

Відповідно середній темп приросту визначають як:

.                                                                  (1.1.9)

Показник середнього темпу зростання, обчислюваний за формулою середньої геометричної (1.1.8), має суттєві недоліки, оскільки грунтується на зіставленні останнього та початкового рівнів часового ряду, проміжні рівні до уваги не беруться. У разі суттєвого коливання рівнів використання середнього геометричного темпу зростання для статистичного аналізу може призвести до серйозних помилок, внаслідок чого реальна тенденція часового ряду буде викривлена.

Сучасні  способи розрахунків середнього темпу зростання певною мірою позбавлені недоліків середньої геометричної. Наприклад, для розрахунків середнього темпу зростання пропонується використовувати формулу:

,                                                                           (1.1.10)

де , − згладжені за рівнянням тренду (рівнянням кривої зростання) перший та останній рівні часового ряду. Порядок побудови моделі тренду розглянуто у розділі 2.2 частини ІІ. У моделі тренду враховано коливання проміжних рівнів часового ряду, тому обчислені за нею значення та й середній темп зростання  (1.1.10) точніше характеризуватимуть зміну економічного явища впродовж інтервалу дослідження.

Якщо тенденція часового ряду не змінюється, використовують характеристику середнього рівня ряду. В інтервальному ряду динаміки з однаково розташованими в часі рівнями середній рівень ряду обчислюють за формулою простої середньої арифметичної (тут і далі додавання ведеться за усіма періодами спостережень):

.                                                                          (1.1.11)

Якщо  інтервальний ряд має неоднаково розташовані в часі рівні, тоді середній рівень ряду (так звану середню хронологічну) обчислюють за формулою зваженої арифметичної середньої, де вагою є тривалість часу (наприклад, кількість років), упродовж якого рівень постійний:

,                                                                         (1.1.12)

де t  − кількість періодів часу, для яких значення рівня не змінюється.

Для моментального ряду з однаково розташованими в часі рівнями середню хронологічну розраховують за формулою:

,                                (1.1.13)

де п  − кількість рівнів ряду.

Середню хронологічну для моментального часового ряду з неоднаково розташованими в часі рівнями розраховують за формулою:

.                     (1.1.14)

Тут п − кількість рівнів ряду, а t період часу, що відокремлює 1-й рівень ряду від (t+1)-го рівня.

Коригування рівнів часового ряду. Часовий ряд правильно відображає об’єктивний закон зміни економічного показника, коли рівні цього ряду є порівнянними, однорідними, сталими та мають достатню сукупність спостережень. Невиконання однієї із цих умов робить некоректним застосування математичного апарату для аналізу часового ряду.

Порівнянність означає, що рівні часових рядів повинні мати  однакові одиниці вимірювання, однакову періодичність обліку окремих спостережень, однаковий ступінь агрегування, обчислюватися за тією самою методикою. В економіці й соціології найпоширенішими є такі причини непорівнянності:

– за територією, внаслідок зміни кордонів регіону, за яким збирають статистичні дані;

– за колом охоплення об’єктів і підпорядкуванням або формою власності. Наприклад, внаслідок переходу частини підприємств конкретного об’єднання до іншого;

– за часовим періодом, коли дані кількох років наведено за станом на різні дати, або місяці мають різну тривалість, на порівнянність економічних і соціологічних даних впливають свята;

– через розбіжність у структурі одиниць сукупності, для якої їх обчислено. Наприклад, дані стосовно кількості населення залежать не лише від зміни кількості народжених і померлих, а й від зміни вікового складу населення впродовж періоду спостереження;

– за вартісними показниками. Навіть у тих випадках, коли значення цих показників фіксуються в незмінних цінах, їх часто важко зіставити.

Існують й інші причини. Непорівнянність часових рядів неможливо усунути лише формальними методами, тому на неї зважують в процесі змістовного тлумачення рядів спостережень і результатів їхнього статистичного аналізу.

Однорідність означає відсутність нетипових, аномальних спостережень, а також викривлень тенденції. Під аномальним рівнем розуміють окреме значення рівня часового ряду, яке не відповідає потенційним можливостям економічної системи, що вивчається, і яке, залишаючись рівнем ряду, чинить суттєвий вплив на значення основних характеристик часового ряду. Формально аномальність виявляється як несподіваний стрибок (або спад) із подальшим поступовим встановленням попереднього рівня. Аномальність призводить до зміщення оцінок і, отже, до спотворення результатів аналізу. Причинами аномальних спостережень можуть бути помилки технічного порядку, або помилки першого роду: агрегування та дезагрегування показників, під час передання інформації та з інших технічних причин. Помилки першого роду слід виявляти і виправляти. Крім того, аномальні рівні в часових рядах можуть виникати через помилки другого роду: значення відображають об’єктивний розвиток процесу, але істотно відхиляються від загальної тенденції розвитку процесу; значення, що виникають через зміну методики обчислення, тощо. Ці помилки трапляються епізодично, тобто дуже рідко, і не підлягають усуненню. Для виявлення аномальних рівнів часових рядів використовують методи, призначені для статистичних сукупностей (метод Ірвіна тощо). Засоби описової статистики та обчислення їх за даними вибіркових спостережень наведено в табл.1.1.5.

Таблиця 1.1.5

Основні статистичні характеристики випадкової вибірки

Характеристики	Оцінки вибіркових значень
1	2
1. Середні значення: арифметичне геометричне гармонійне
2. Дисперсія Середньоквадратичне відхилення (СКВ)	(незміщена оцінка)
3. Середнє абсолютне лінійне відхилення ()
4. Початкові моменти: другого, третього, четвертого порядку	;;
5. Моменти центральні: другого,   третього, четвертого порядку	;
9. Коефіцієнт асиметрії його незміщена оцінка   СКВ
10. Показник ексцесу його незміщена оцінка СКВ
11. Коефіцієнти варіації: за розмахом за середнім абсолютним лінійним відхиленням   за СКВ медіана мода   мінімальне значення ряду максимальне значення ряду розмах	– характеризує величину, яка найчастіше спостерігається ymin ymax R= ymax-ymin

 

Метод Ірвіна грунтований на порівнянні сусідніх значень ряду і розрахунку характеристики , яка дорівнює:

; t=2,3,…,n,                                                               (1.1.15)

де − оцінка середньоквадратичного відхилення вибіркового ряду , яка розраховується з використанням формул:

, .

Розрахункові значення , тощо порівнюють із критичним значенням , і якщо вони не перевищують критичне, то відповідні рівні вважаються нормальними. Критичні значення для рівня значущості α = 0,05 (помилка 5%) наведено в табл.1.1.6.

Таблиця 1.1.6.

п	2	3	10	20	30	50	100
	2,8	2,3	1,6	1,3	1,2	1,1	1,0

Критерій Ірвіна не «сприймає» аномальність, якщо вона виявляється в середині ряду зі стрімкою динамікою, тобто коли стрибок великий, але не перевищує рівнів наприкінці періоду спостережень, оскільки величина характеризує відхилення значень показника від середнього рівня за всією сукупністю спостережень.

Модифікація цього методу пов’язана із послідовним розрахунком не за всією сукупністю, а за трьома спостереженнями. Так, для всіх або лише для підозрюваних в аномальності рівнів розраховують оцінки середнього  і середньоквадратичного відхилення для двох сусідніх із ними значень:

, t=2,3,…n-1 ,                                                                 (1.1.16)

      ,                                                               (1.1.17)

Обчислюють величину , t=2,3,…,n.                               (1.1.18)

Розраховані ковзні значення порівнюють із критичними значеннями (див. таблицю 1.1.6.)  для .

Викривлення тенденції свідчить про зміну закономірності розвитку процесу або про зміну методики обчислення значень показника. Якщо точно встановлено, що причиною аномальності є помилки першого роду, то аномальні спостереження замінюють або простою середньою арифметичною двох сусідніх рівнів ряду, або відповідними значеннями за кривою, що згладжує цей часовий ряд. Не перевіряють часові ряди з періодом сезонності, більшим за одиницю, а також кінцеві рівні періоду спостережень.

Якщо значення наприкінці часового ряду “випадає” із загальної тенденції, то без додаткової інформації стосовно причин “випадіння” в кінці ряду неможливо визначити, чи це спостереження аномальне, чи відбувається зміна тенденції. У цьому разі важливо провести якісний аналіз змін, що відбуваються, або дочекатися надходження результатів нового спостереження.  Якщо викривлення тенденції пояснюється зміною методики обчислення показника, то рівні, що передують викривленню тенденції, можуть бути використані  для оцінки характеристик динаміки і побудови моделі за умови, що вони будуть обчислені за новою методикою. Якщо таке обчислення неможливе, ці рівні ряду треба виключити з розгляду. Якщо викривлення тенденції відображає зміну закономірності розвитку процесу, то за інформаційну базу для статистичного аналізу можна взяти лише значення, що відповідають останнім змінам.

Стійкість часового ряду відбиває перевагу закономірності над випадковістю у зміні рівнів ряду. На графіках стійких часових рядів унаочнюється закономірність, а на графіках несталих рядів зміни послідовних рівнів постають хаотичними, тож пошук закономірностей формування значень рівнів таких рядів марний.

Достатня сукупність спостережень насамперед характеризує повноту даних. Достатня кількість спостережень визначається залежно від мети дослідження динаміки. Якщо метою є описовий статистичний аналіз, то за період дослідження можна обрати будь-який, на власний розсуд. Якщо мета дослідження – побудова прогнозної моделі, тоді для статистичного аналізу, який розглядає незалежні спостереження з однаковим розподілом, кількість рівнів динамічного ряду має бути якомога більшою і, як правило, не менш як утричі має перевищувати період упередження прогнозу й становити більше 7. У разі використання квартальних або місячних даних для дослідження сезонності  й прогнозування сезонних процесів часовий ряд має містити квартальні або місячні дані не менш як за чотири роки, навіть якщо складають прогноз на 1 – 2 квартали (місяці).

У методах нелінійної динаміки підхід до формування достатньої кількості даних відрізняється від прийнятого більшістю статистиків. У стандартній статистичній теорії чим більше даних точок спостережень, тим краще, бо спостереження передбачаються як незалежні. Нелінійні динамічні системи характеризуються процесами із довготривалою пам’яттю. Тому для них охоплення більшого періоду часу є важливішим, ніж збільшення кількості точок спостережень. Наприклад, щоденна вибірка за чотири роки, або 1040 спостережень, не дадуть такого результату, як щомісячні дані за сорок років, або загалом 480 спостережень. Причина полягає в тому, що щоденні дані утворюють лише один чотирирічний цикл, а щомісячні – десять циклів. Нелінійні процеси мають так звану “стрілу часу”. Збільшення “частоти” даних часто навіть ускладнює аналіз і не поліпшує значущості результату.

1.2. Випадкові процеси і часові ряди 

Основні елементи теорії випадкових процесів. Для аналізу часового ряду порядок у послідовності є суттєвим, тобто час виступає одним із визначальних чинників. Це відрізняє часовий ряд від звичайної випадкової вибірки, де індекси вводять лише для зручності ідентифікації. Принциповою відмінністю часового ряду від простих статистичних сукупностей є :

по-перше, рівні часового ряду не є незалежними. Інакше кажучи, якщо майбутні значення змінної можна визначити, то вони є функцією від минулих значень цієї змінної;

по-друге, рівні часового ряду неоднаково розподілені. Закон розподілу ймовірностей цих випадкових величин і, зокрема, їхні математичні сподівання та дисперсії, можуть залежати від часу.

Отже, не можна поширювати властивості та правила статистичного аналізу випадкових вибіркових спостережень на часові ряди. Порушення умови незалежності між спостереженнями призводить до негативних наслідків застосування цих методів. Наприкінці 1980-х – на початку 1990-х років дослідники остаточно переконалися, що лише врахування часової структури даних про реальні економічні процеси дають змогу адекватно відобразити їх в економіко-математичних моделях. Усвідомлення цього факту зумовило перегляд багатьох макроекономічних теорій і побудов та бурхливий розвиток специфічних методів аналізу таких даних, що дістали назву аналіз часових рядів.

Потужним математичним апаратом дослідження зміни соціально-економічних показників у їхній динаміці нині є теорія випадкових (стохастичних) процесів. Випадковий процес описують деякою функцією від часу, значення якої в будь-які моменти часу є випадковими величинами. Наведемо основні поняття та визначення теорії випадкових процесів, необхідні для подальшого аналіза часових рядів.

Реалізацією випадкового процесу називають послідовність результатів спостережень  певного економічного процесу в моменти часу .

Динамічним, або часовим рядом (time series) будемо називати послідовність спостережень , одержаних у рівновіддалені моменти часу, а відповідну йому ймовірнісну модель – дискретним випадковим або однофакторним стохастичним процесом.

Оскільки випадковий дискретний процес являє собою сукупність випадкових величин, то його найповнішою статистичною характеристикою є сумісна функція розподілу, або функція щільності розподілу. Щоб задати всі ймовірнісні властивості часового ряду, потрібна сукупність функцій розподілу, а саме одномірна,  двомірна, трьохмірна функції розподілу тощо: . Індекси у величин означають, що випадкові величини розглядаються в моменти часу і вони мають сумісну функцію розподілу. Якщо взяти інші моменти часу, то функція розподілу буде іншою. Така сукупність функцій розподілу цілковито характеризує випадковий процес.

Стаціонарні процеси. Економетричне моделювання відбувається, як правило, на підставі лише однієї реалізації випадкового процесу, тож ясно, що про оцінювання сукупності усіх функцій розподілу взагалі годі казати. Окрім того, якщо процес поводиться так, що його основні статистичні характеристики із часом змінюються, то за короткий проміжок часу спостережень про нього взагалі нічого не можна сказати. Проблема втрачає гостроту, якщо розглядати вужчий клас випадкових процесів, який дістав назву стаціонарних випадкових процесів. Під стаціонарністю розуміють такі випадкові процеси, деякі властивості яких не змінюються із часом.

Однією із важливіших властивостей стаціонарного випадкового процесу є ергодичність. Вона полягає у тому, що кожна окрема реалізація випадкового процесу є так би мовити “повноважним” представником усієї сукупності можливих реалізацій. Звідси для ергодичних процесів основні характеристики можна приблизно розраховувати не за кількома реалізаціями, як це робиться в загальному випадку, а за будь-якою однією реалізацією за доволі тривалий проміжок часу. В практичних розрахунках розглядають стаціонарний процес в широкому сенсі.

Стаціонарний часовий ряд у широкому сенсі це процес, для якого математичне сподівання та дисперсія існують і є сталими величинами, що не змінюються у часі, а автокореляційна (автоковаріаційна) функція залежить лише від різниці між двома моментами часу і не залежить від конкретного періоду часу. Тобто для реалізації випадкового процесу основні моменти залишаються постійними й обмеженими при зміні часу , для якого вони розраховуються, а саме:

математичне сподівання: , для всіх ;

дисперсія: , для всіх ;

автоковаріація порядку:

, для всіх .

Для отримання практичних оцінок для часових рядів користуються такими формулами:

математичне сподівання: ;

дисперсія: ;                                                            (1.2.7)

автоковаріація порядку:  .

Зрушення в часі називають часовим лагом. Зауважимо, що  , коли = 0, дорівнює дисперсії: =. При цьому . Можна розглядати функцію як усі можливі значення автоковаріацій, де перебирає цілочисельні значення від до . Сукупність значень автоковаріацій за всіх можливих значень називають  автоковаріаційною функцією випадкового процесу. Автоковаріаційна функція стаціонарного часового ряду залежить лише від різниць моментів часу (). Ця функція парна і досить розглядати невід’ємні .

Коефіцієнт автокореляції між зрушеними на рівнями часового ряду – це автоковаріація, розділена на корінь із добутку двох дисперсій, та оскільки дисперсія стала, отримуємо просто або . Розраховують коефіцієнт автокореляції за формулою:

.                                                                                                     (2.1.8)

Вираз (2.1.8) визначає  автокореляційну функцію (АКФ) часового ряду, яка показує наскільки статистично залежними є значення часового ряду для різних зрушень у часі (наприклад, для річних спостережень рік чи два роки тощо). Автокореляційна функція стаціонарного часового ряду залежить лише від різниці між двома моментами часу , і є парною функцією, тобто =. Задаючи різні значення = 1, 2, 3,…, отримують послідовність значень , , ,…. Графік автокореляційної функції називають корелограмою. За корелограмою можна визначити запізнення, із яким зміна показника позначається на його наступних значеннях.

У широкому сенсі оцінки наведених статистик є консистентними, тобто для них існує межа щодо імовірності, яка збігається з їхніми справжніми значеннями для генеральної сукупності. Далі замість стаціонарності у широкому сенсі будемо просто говорити стаціонарність, оскільки інші різновиди стаціонарності не розглядатимуться. 

Приклад 1.2.1. На рис.1.2.2 зображено часовий ряд щоквартальних значень доходів консолідованого бюджету України (млн грн) із 1999 до 2002 р. Цей показник за 4 роки збільшився із 6008,5 до 17298,2. Аналіз середньої й середнього квадратичного відхилення, зроблений за кожен рік, свідчить, що середня величина і середнє квадратичне відхилення впродовж першого року будуть нижчими, ніж впродовж другого року тощо, і очевидно, що в останньому році, коли показник зростає до 17298,2 млн грн, його середній рівень буде вищий, ніж за перший рік.

Величина дисперсії й середнього квадратичного відхилення може бути функцією від значення показника. Отже, дисперсія показника, що коливається навколо 6008,5 (значення першого рівня), цілком може бути нижчою за дисперсію показника, що коливається навколо позначки 17298,2 (значення останнього рівня). Коваріація також може залежати від рівня значень даних, що аналізуються. У такому разі існує коваріація між послідовними спостереженнями.

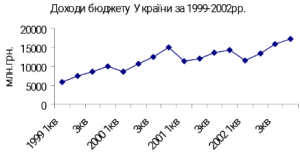
Рис.1.2.2. Нестаціонарний часовий ряд

На рис.1.2.3 показано часовий ряд доходів консолідованого бюджету, виражений у відсотках до ВВП. Доходи, виражені у відсотках до ВВП, характеризуються постійними середньою, середнім квадратичним відхиленням і коваріацією спостережень, яка залежить суто від інтервалів між спостереженнями. Очевидно, ряд значень показника доходів бюджету не є стаціонарним, тоді як ряд значень відсотка до ВВП доходів бюджету може бути стаціонарним.

Інтуїтивно можна очікувати, що небагато (якщо взагалі знайдуться) часових рядів соціально-економічних показників будуть стаціонарними, оскільки зростаючі й спадні значення є головною рисою соціально-економічних показників. У контексті стаціонарних і нестаціонарних часових рядів наведемо приклади простіших однофакторних стохастичних процесів.

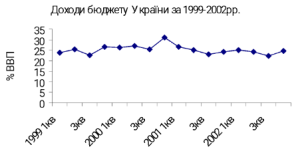
Рис.1.2.3.  Часовий ряд доходів консолідованого бюджету, виражений у відсотках до ВВП

 

Білий шум (white noise). Білим шумом називають часові ряди, рівні яких мають середню, що дорівнює нулю, сталу дисперсію та нульову коваріацію послідовних спостережень, тобто нульову автокореляцію. Наприклад, залишки регресії, що задовольняють умовам теореми Гауса-Маркова є “білим шумом”: ; ; за .

Наведене визначення білого шуму характеризує його як стаціонарний ряд. Хоча стаціонарний ряд необов’язково буде білим шумом, оскільки може мати середню або коваріацію, відмінні від нуля.

Якщо ~, то йдеться про гаусівський білий шум, хоча змінна білого шуму не обов’язково підпорядковується закону нормального розподілу. Найкращим передбаченням або прогнозом білого шуму є його нульове середнє значення. Білий шум відіграє важливу роль в аналізі часових рядів. На практиці білий шум трапляється не надто часто, але він утворює складніші процеси. Прикладом цього є процес випадкового блукання.

Випадкове блукання (Random walk). Іноді його називають броунівським рухом. Це стохастичний процес, де зміна рівня ряду, скажімо, рівня інфляції, досягається додаванням до нього випадкової змінної εt із постійною дисперсією та середнім, що дорівнює нулю. Випадкове блукання задається так:

,                                                                                     (1.2.9)

де − білий шум. Цей процес можна розглядати як авторегресію із коефіцієнтом 1. Зазначимо, що лише має нульову середню і постійну дисперсію.

Термін “випадкове блукання” виник у зв’язку із жартівливою задачкою: якщо в поле випустити п’яного, то де він опиниться через деякий час? Результат – якщо п’яний блукає випадково, то його слід очікувати на тому самому місці, тобто в середньому його місцезнаходження  не зміниться.

За умови наявності певної початкової точки підстановка у (1.2.9) значень змінної за попередні моменти часу дає вираз  , який за t, що прямує до нескінченності, включатиме необмежену кількість доданків , кожен із яких має нульове математичне сподівання та ненульову дисперсію .

Обрахуємо математичне сподівання процесу випадкового блукання: , тобто математичне сподівання задовольняє умові стаціонарності.

Дисперсія процесу випадкового блукання дорівнює: . Після розкриття дужок подвоєні добутки після узяття математичного сподівання будуть дорівнювати нулю, і залишиться математичне сподівання суми квадратів. Враховуючи властивості дисперсії білого шуму, одержимо   . Отже, процес випадкового блукання не стаціонарний, оскільки дисперсія зростає із часом.

Прогноз такого процесу на 1 крок вперед дорівнює . Але незалежно від . Отже прогноз на крок вперед становить: . На два кроки уперед: тощо. Прогноз на кроків вперед становитиме:

.

Хоча величина прогнозної оцінки із зростанням періоду упередження прогнозу залишається постійною, дисперсія помилки прогнозу зростає. Так, помилка прогнозу на один крок вперед дорівнює та її дисперсія дорівнює . Для прогнозу на два кроки вперед , а дисперсія , оскільки та – незалежні. Аналогічно для прогнозу на кроків вперед дисперсія помилки прогнозу становитиме . Середньоквадратичне відхилення прогнозу зростає пропорційно і можна оцінити інтервал надійності прогнозу.

Якщо рівняння , де збурення  є білим шумом, переписати як , одержимо процес білого шуму. Приріст, або першу різницю (first difference), можна розглядати як інший часовий ряд , який є стаціонарним. Перехід до перших різниць є розповсюдженим засобом зведення  нестаціонарного часового ряду до стаціонарного.

Іноді випадкове блукання може передбачати елемент зсунення. Зсунення означає тенденцію (дрейф). Отже, випадкове блукання зі зсуненням – це випадкове блукання із дрейфом. Наприклад:

,                                                                           (1.2.10)

де − стала величина.

Тепер та .

Середньоквадратичне відхилення прогнозу у цьому разі не зміниться, оскільки: .

Прогноз зростає лінійно за і інтервал надійності прогнозу розширюється пропорційно .

Середнє значення перших різниць становить швидкість зростання фактичного ряду спостережень, при цьому кожна зміна не залежить від усіх попередніх змін і має ідентичний розподіл імовірностей. .

Марківський процес. Марківськими називають процеси, в яких стан об’єкта в кожен наступний момент часу визначається станом поточного моменту і не залежить від того, яким шляхом  об’єкт досяг поточного стану. Це стаціонарна послідовність незалежних, однаково розподілених випадкових величин. У термінах кореляційного аналізу часових рядів марківський процес можна описати таким чином: існує статистично значущий кореляційний зв’язок початкового ряду із рядом, зрушеним на один часовий інтервал, і цей зв’язок відсутній із рядами, зрушеними на два, три тощо часові інтервали. В ідеальному випадку ці коефіцієнти кореляції  дорівнюють нулю.

За допомогою рівняння авторегресії такий ряд можна представити як:

або ,                                                            (1.2.11)

розкладаючи , одержуємо: тощо. Очевидно, що залежить від усіх минулих (але не майбутніх) . Якщо , то й . Знайдемо добуток (1.2.11) на і визначимо математичне сподівання:

або ,

остаточно , тобто є першою автокореляцією процесу.

розділимо на :.

Отже, всі кореляції марківського процесу можна виразити через першу автокореляцію.

Окрім марківських процесів з-поміж стаціонарних процесів авторегресії часто трапляються процеси Юла, в яких враховано авторегресію не лише першого, а й другого порядку, тобто .

Розкладення (декомпозиція) часового ряду. Реальні часові ряди в економіці, як правило, є динамічно нестабільними, отже – не стаціонарними, і поняття стаціонарності процесу часто є лише зручною абстракцією для застосування статистичних методів. Кожен рівень часового ряду формується під впливом великої кількості чинників, які відображають закономірність і випадковість його формування. В аналізі часових рядів прийнято представляти часовий ряд у вигляді суми систематичної складової (середньої) і випадкового відхилення від неї:

,                                                                                              (1.2.12)

де − невипадкова функція часу (детермінована частина);

−  випадкова, недетермінована частина.

Завдання  розкладення часового ряду полягає в аналізі чинників, що впливають на значення його рівнів, у вирізненні серед них головних і другорядних (випадкових), а потім серед головних – еволюційних, періодичних, сезонних тощо.

• Еволюційні чинники визначають загальний напрям розвитку економічного показника, провідну його тенденцію. Тенденція – це невипадкова складова часового ряду, яка змінюється повільно, і описується за допомогою певної функції , яку називають функцією тренду або просто трендом. Тренд відображає вплив на економічний показник деяких постійних чинників, дія яких акумулюється в часі. У широкому сенсі під трендом розуміють будь-який упорядкований процес, що відрізняється від випадкового, тобто функцію у (1.2.12). Іноді під трендом розуміють також зміщення у часі математичного сподівання. Відносно припускається, що це певна гладка функція, ступінь гладкості якої заздалегідь не відомий. Під ступінню гладкості розуміють мінімальну ступінь поліному, що найкраще згладжує компоненту . На рис. 1.2.4 а) зображено умовний часовий ряд із тенденцією, що лінійно зростає.
• Серед чинників, що визначають регулярні коливання ряду, розрізняють такі:

Сезонні, що відповідають коливанням, які мають періодичний або близький до нього характер упродовж одного року. Наприклад, ціни на сільгосппродукцію влітку вищі, ніж взимку; рівень безробіття в курортних містах у зимовий період зростає відносно до літнього. Вони можуть охоплювати причини, пов’язані з діяльністю людини (свята, відпустки, релігійні традиції тощо). Так, у ряду щомісячних даних слід очікувати наявності сезонних коливань із періодом 12, у квартальних рядах – із періодом 4. На рис. 1.2.4 б) зображено умовний часовий ряд, який містить лише сезонну компоненту. Результат дії сезонних чинників моделюють за допомогою функції .

Циклічні (кон’юнктурні) коливання схожі на сезонні, але виявляються на триваліших інтервалах часу. Циклічні коливання пояснюються дією довготермінових циклів економічної, демографічної або астрофізичної природи. Наприклад, за багаторічними спостереженнями активність сонця має циклічність у 10,5 – 11 років, причому сплески сонячної радіації впливають на врожайність зернових культур, репродуктивну властивість тварин тощо. Отже динаміка показника містиме характерні зміни, що повторюються з однаковою циклічністю. Результат дії циклічних чинників моделюють за допомогою функції .

Тренд, сезонна і циклічна компоненти не є випадковими, тому їх називають систематичними компонентами часового ряду.

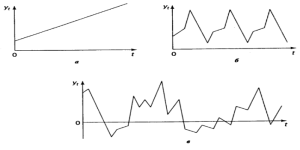
Рис.1.2.4.Головні компоненти часового ряду: а − тренд, що зростає; б − сезонна компонента; в − випадкова компонента

• Випадкові чинники не підлягають вимірюванню, але неминуче супроводжують будь-який економічний процес і визначають стохастичний характер його елементів. До випадкових чинників можна віднести помилки вимірювання, випадкові збурення тощо. Деякі часові ряди, наприклад стаціонарні, не мають тенденції й сезонної складової, кожен наступний рівень їх утворюється як сума середнього рівня ряду і випадкової (додатної або від’ємної) компоненти. Приклад такого ряду демонструє рис. 1.2.4 в). Результат впливу випадкових чинників позначається випадковою компонентою εt, яку обчислюють як залишок або похибку, що залишається після вилучення з часового ряду систематичних компонент. Це не означає, що така складова не підлягає подальшому аналізу, оскільки містить лише хаос.

За декомпозицією Вольда суто недетермінований  стаціонарний в широкому сенсі випадковий процес можна записати у вигляді:

,                                               (1.2.13)

де − детермінована складова або математичне сподівання цього процесу, − білий шум з обмеженими математичним сподіванням та дисперсією. Розкладення Вольда (1.2.13) ще називають лінійним фільтром.  Начебто білий шум пропустили через лінійний фільтр. Це означає, що, не втрачаючи ціле, обмежуються зручним лінійним представленням й переходять до вивчення стаціонарних процесів. Щоб вираз (1.2.13) мав сенс, повинна виконуватися умова збіжності за імовірністю, оскільки підсумовуються випадкові величини. Ця умова записується, як . Припускається, що =1. Чим більший ваговий коефіцієнт , тим більший вплив випадкового збурення в момент на поточний момент t.

Аналіз випадкової компоненти є важливою інформативною частиною дослідження часових рядів. Пояснюється це тим, що в короткотерміновому та певною мірою середньотерміновому прогнозуванні результати прогнозу тісно пов’язані із випадковою компонентою, тоді як у довготерміновому прогнозуванні головну увагу приділяють визначенню тенденції й взаємозв’язків між чинниками.

Очевидно, реальні дані цілковито не відповідають лише одній із наведених функцій, тож часовий ряд , можна уявити у вигляді розкладення:

,                                                                 (1.2.14)

або різноманітних поєднань окремих функцій. Однак завжди припускають обов’язкову наявність випадкової складової. Розкладення (декомпозиція) часового ряду відбувається за такими варіантами моделей:

модель тренду , ;                                                  (1.2.15)

модель сезонності , ;                                           (1.2.16)

тренд-сезонна модель , .                               (1.2.17)

Моделі тренду й сезонності (тренд-сезонні) можуть відображати як відносно постійну сезонну хвилю (цикл), так і динамічно змінювану залежно від тренду. Перша форма − (1.2.14−1.2.17) належить до адитивних, друга (, , (1.2.18)) − до мультиплікативних моделей.

Моделі для врахування циклічних чинників будують аналогічно до тренд-сезонних, тільки замість сезонної складової вводять циклічну.

Процес окремого обчислення функцій і називають фільтрацією компонент часового ряду . Процедура оцінювання детермінованої частини разом з усіма невипадковими компонентами має назву згладжування часового ряду.

Успішне розв’язання завдань виявлення й моделювання дії розглянутих складових чинників є підґрунтям, відправним пунктом для зрозуміння механізму формування соціально-економічного процесу та його прогнозування.

Утім, слід пам’ятати, що операція розкладення часового ряду, яка є допустимою з математичної точки зору й корисною для моделювання динаміки зміни показників у часі, подеколи може ввести в оману. Зокрема, за такого підходу дуже спрощеним може виявитися припущення стосовно незалежного впливу названих компонент, їхньої чіткої структури.

Типи нестаціонарних часових рядів. За видом нестаціонарності часові ряди, що застосовують в економічній практиці, розподіляють на ряди типу: TS, DS, тренд-сезонні, нелінійні.

Часовий ряд типу TS (trend stationary process). До цього типу відносять нестаціонарні часові ряди із детермінованим поліноміальним трендом , де поліном ступеня від , а − стаціонарний процес, який не обов’язково є білим шумом.  Наприклад, простий лінійний тренд . Тут нестаціонарна змінна виражена через детермінований, тобто невипадковий тренд. Попри те, що додавання стаціонарної змінної призводить до коливань навколо тренду і робить випадковою, ми, власне, маємо інформацію тільки про середнє значення =, тобто часовий ряд характеризується наявністю тренду в середньому значенні. Отже, ані поточна, ані минулі події не змінюють довготермінових прогнозів цього процесу. Вплив випадкового збурення (поточний шок) забувається одразу на наступному кроці (). Похибка довготермінового прогнозу буде мати обмежену дисперсію , тому невизначеність є обмеженою навіть у далекому майбутньому.

Нестаціонарний процес типу TS зводять до стаціонарного за допомогою декількох методів. Наприклад, для лінійного тренду перехід до стаціонарності може відбуватися:

• шляхом виділення лінійного тренду. Наприклад, будують лінійну регресію за часом і  розглядають стаціонарний залишок ;

– включенням в регресію лінійного тренду;

• взяттям перших різниць: різниці двох суміжних рівнів часового ряду

(1.2.20)

є першими різницями ряду , або . Звідси  , де − випадкова величина, розподіл якої цілком визначається розподілом величини . Окрім того, перші різниці часового ряду з лінійною тенденцією мають постійне математичне сподівання, що дорівнює певній константі , не залежній від .

Загалом якщо часовий ряд має тенденцію, що виражається через поліном ступеня , то різниці порядку

(1.2.21)

є випадковими величинами із постійним математичним сподіванням. У цьому разі .

Якщо тенденція часового ряду відповідає експоненціальному або степеневому тренду, то метод послідовних різниць слід застосовувати не до початкового ряду, а до його логарифмів.  Наприклад, процес у своєму розвитку наближається до певної величини і може бути представлений у вигляді

, ,                                                                                  (1.2.22)

де − аналогічна (1.2.20). Тоді процес, утворений із величин  , має постійне середнє () і може бути зведений до стаціонарного процесу авторегресії.

Часовий ряд типу DS (differencing stationary process). Це ряди без періодичної складової й тенденції зростання, але наявність тренду в дисперсії засвідчує їхню нестаціонарність. Прикладом таких рядів є процес випадкового блукання . Як вже зазначалося, цей процес накопичує випадкові збурення від усіх попередніх шоків, тобто має нескінченну пам’ять. Такий процес описують стохастичним трендом і зводять до стаціонарного шляхом взяття першої різниці, звідси й відповідна назва.

Тренд-сезонні часові ряди окрім тренду містять чітко виражені сезонні коливання, які, своєю чергою, спричинюють нестаціонарність. Якщо процес включає періодичні (сезонні) коливання навколо середнього значення із періодом , тобто

(1.2.23)

із точністю до випадкової складової, то у цьому разі різниці через часових інтервалів представляють стаціонарний процес

, де – ,                                               (1.2.24)

середнє значення якого співпадає із середнім значенням початкового ряду.

Амплітуда сезонних коливань може зростати з часом і не обов’язково лінійно. Ці ряди характеризуються наявністю тренду в середньому значенні й дисперсії.

Нелінійні динамічні процеси. До цього типу відносять часові ряди зі складною структурою, вони мають тренд і містять різні види коливань, зокрема сезонні та циклічні. Структуру таких рядів взагалі не можна описати за допомогою відомих функцій, оскільки для різних ділянок часового ряду набір цих функцій буде різним, тобто в цьому разі можна говорити про ряди зі змінною структурою, які характерні для нелінійних динамічних процесів. Вони спостерігаються в динаміці цін на ринках капіталу тощо. Лише в останні роки завдяки розвитку математичних методів нелінійної динаміки і комп’ютерних технологій з’явилася можливість досліджувати такі процеси. У певному аспекті [29] будь-який динамічний процес зрештою є детермінованим і моделювання його як реалізації випадкового процесу є зручним спрощенням. Невипадковий часовий ряд відображає невипадкову природу впливів. Стрибки даних відповідають стрибкам впливових чинників і відбивають властиву їм кореляцію.  Детерміновані процеси, що виглядають як випадкові, у теорії нелінійностей називають детермінованим хаосом. Добре відомо, що просте детерміноване нелінійне різницеве рівняння може породжувати надзвичайно складні часові траєкторії, які видаються випадковими. Наприклад, рівняння, яке трапляється в аналізі фінансових ринків  , де є ціною облігацій. У багатьох економічних застосуваннях значення параметру лежить між 1 та 4, таким чином виключають від’ємні значення рівноваги для і уникають прямування процесу до нескінченності. При зміні від 1 до 4 динаміка системи зазнає суттєвих змін. Наприклад, для 1<<3, за будь-яким відхиленням від , динаміка процесу прямує до рівноваги . Разом з тим, для 3,75<<4 буде спостерігатися нескінченна кількість циклів із різною періодичністю і нескінченне число положень рівноваги з еволюцією процесу залежно від початкового його стану. Такий тип поведінки називається “хаосом”. Властивістю такого процесу є те, що хоча він детермінований, випадкове блукання є задовільною моделлю для описання механізму породження даних. У цьому випадку зміни неможливо передбачити, хоча всю траєкторію розвитку процесу цілком можна передбачити.

1.3. Ідентифікація часових рядів. 

Структуру часового ряду в деяких випадках можна визначити графічно. Це стосується, наприклад, таких компонент ряду, як тренд і сезонні коливання. Однак чисту випадковість інколи помилково сприймають як наявність певної структури, і навпаки, за шумом можна не розгледіти існування структури. Тому потрібні методи або інструменти, за допомогою яких можна було б звести нанівець ефект впливу шуму, після чого з’ясувати характеристики ряду, необхідні для побудови відповідної прогнозової моделі. Як правило, спочатку з’ясовують, із яким процесом доведеться працювати – стаціонарним чи нестаціонарним. Для будь-якого нестаціонарного ряду важливо визначити ознаку його нестаціонарності: чи описується він детермінованим трендом, чи є інтегрованим процесом і описується стохастичним трендом (лінійним або нелінійним), визначити наявність періодичної складової.

Перевірка стаціонарності часового ряду. Стаціонарні часові ряди передбачають, що процес породження наявних даних є лінійним. Вони не мають тренду або періодичної зміни середнього та дисперсії.

Перевірку гіпотез стосовно сталості середнього значення та дисперсії  часового ряду можна здійснити кількома способами. Найпростішими з них є перевірка значущої відмінності двох середніх значень для деяких підмножин вибірки (наприклад, для першої та останньої третин усього обсягу даних) за – критерієм (критерій перевірки гіпотези про рівність середніх двох нормально розподілених вибірок) і для дисперсії, якщо справедливе припущення про нормальний розподіл, можна використати F-критерій. Розглянемо два поширені методи: метод перевірки різниць середніх рівнів і метод Форстера-Стьюарта.

М е т о д  п е р е в і р к и  р і з н и ц ь  с е р е д н і х  р і в н і в.  Реалізація цього методу передбачає такі чотири кроки.

Крок перший. Вхідний часовий  ряд розподіляють на дві приблизно однакові за кількістю спостережень частини: в першій частині п1 першої половини рівнів вхідного ряду, у другій – решта рівнів п2 ().

Крок другий. Для кожної із цих частин розраховують середні значення й дисперсії: ; ;  ; .

Крок третій. Перевірка рівності (однорідності) дисперсій обох частин ряду за допомогою F-критерію, що порівнює розрахункове значення цього критерію:

(1.3.1)

із табличним (критичним) значенням критерію Фішера Fα із заданим рівнем значущості α. Якщо розрахункове значення F менше за табличне Fα, то гіпотезу про рівність дисперсій приймають і можна переходити до четвертого кроку. Якщо F більше або дорівнює Fα, гіпотезу про рівність дисперсій відхиляють і доходять висновку, що цей метод не дає відповіді щодо наявності тренду.

На четвертому кроці перевіряють гіпотезу про відсутність тренду за допомогою t-критерію Стьюдента. Для цього визначають розрахункове значення критерію Стьюдента за формулою:

,                                                                   (1.3.2)

де – оцінка середньоквадратичного відхилення різниць середніх:

.

Якщо розрахункове значення t  менше за табличне tα, то нульову гіпотезу не відхиляють, тобто тренд відсутній, інакше – тренд є. Зазначимо, що в цьму разі табличне значення tα приймають для числа ступенів вільності, яке дорівнює , до того ж цей метод застосовують суто для рядів із монотонною тенденцією. Недолік методу полягає у неможливості правильно визначити існування тренду в тому разі, коли часовий ряд містить точку зміни тенденції у середині ряду.

8Приклад 1.3.1. Застосуємо метод перевірки різниць середніх рівнів для двох часових рядів: доходів консолідованого бюджету (млн грн) і доходів консолідованого бюджету (% ВВП). Для цього початкові часові ряди поділяють на дві однакові частини: перша охоплює 1999-2000 роки, друга – 2001-2002 роки. Кількість кварталів-спостережень в обох частинах однакова: п1 = п2 = 8. Результати розрахунків наведено в табл. 1.3.1. На рівні значущості , тобто з імовірністю 0,95, із числом ступенів вільності k1 = п1-1 = 8-1 = 7 і k2 = п2-1 = 8-1 = 7 табличне значення критерію Фішера дорівнює = 3,79.

 

Таблиця 1.3.1

Доходи	Роки	Середнє значення	Дисперсія	F		t
Млн грн	1999-2000 2001-2002	9860,2 13695,8	8349206 4459451	1,87	2733,44	2,8
% до ВВП	1999-2000 2001-2002	26,0 24,5	6,41 1,92	3,34	2,2	1,37

Для обох часових рядів F розрахункові менші за табличне значення, тобто приймається гіпотеза про рівність дисперсій.

На рівні значущості із числом ступенів свободи п1+п2-2 = 16-2 = 14 табличне значення -розподілу дорівнює = 2,145.

Для часового ряду доходів, виражених у млн грн, t-розрахункове перевищує табличне значення , тобто нульова гіпотеза не приймається, тренд існує.

Для часового ряду доходів, виражених у відсотках до ВВП, t-розрахункове менше за табличне значення , тобто приймається гіпотеза про відсутність тренду.                           8

М е т о д  Ф о р с т е р а-С т ь ю а р т а. Цей метод має більші можливості і дає надійніші результати, ніж попередній. Окрім тренду самого ряду (тренду в середньому), він дає змогу встановити існування тренду дисперсії часового ряду: якщо тренду дисперсії немає, то розкид рівнів ряду постійний; якщо дисперсія збільшується, то ряд «розхитується». Реалізація методу передбачає чотири кроки.

Крок перший. Порівнюють кожен рівень вхідного часового ряду, починаючи із другого рівня, з усіма попередніми, при цьому визначають дві числові послідовності:

(1.3.3)

(1.3.4)

t = 2,3,…,n.

Крок другий. Розраховують величини с і d:

;                                                                                 (1.3.5)

.                                                                                (1.3.6)

Величина c, яка характеризує зміну рівнів часового ряду, набуває значення від 0 (усі рівні ряду однакові) до п-1 (ряд монотонний). Величина d характеризує зміну дисперсії часового ряду і змінюється від [-(п-1)] – ряд поступово згасає, до (п-1) – ряд поступово розхитується.

Крок третій Перевіряється гіпотеза стосовно того, чи можна вважати випадковими: 1) відхилення величини c від математичного сподівання ряду, в якому рівні розташовані випадково, 2) відхилення величини d від нуля. Цю перевірку здійснюють на підставі обчислення t-відношення відповідно для середньої і для дисперсії:

; ;                                                               (1.3.7)

; ,                                                              (1.3.8)

де – оцінка математичного сподівання ряду; 1 – оцінка середньоквадратичного відхилення для величини c; 2 – оцінка середньоквадратичного відхилення для величини d.

Таблиця 1.3.2

п	10	20	30	40
	3,858	5,195	5,990	6,557
1	1,288	1,677	1,882	2,019
2	1,964	2,279	2,447	2,561

Фрагмент розрахованих значень величин , 1 і 2 для різних п наведено в табл. 1.3.2 [25].

Крок четвертий. Розрахункові значення tс i td порівнюють із табличним значенням t-критерію із заданим рівнем значущості tα. Якщо розрахункове значення t  менше за табличне tα, то гіпотезу про відсутність відповідного тренду приймають, у противному разі тренд існує. Наприклад, якщо tс більше табличного значення tα, a td менше tα, то для заданого часового ряду існує тренд у середньому, а тренду дисперсії рівнів ряду немає.

  Приклад 1.3.2. Застосування методу Форстера-Стьюарта для двох часових рядів: доходів консолідованого бюджету (млн грн) та доходів консолідованого бюджету (% до ВВП) дає розрахунки, наведені в табл.1.3.3.

Таблиця 1.3.3

Доходи	∑kt	∑lt	c	d	tс	td
Млн грн	8	0	8	8	3,28	4,07
% до ВВП	4	1	5	3	0,9	1,53

На рівні значущості , тобто з імовірністю 0,95 та з числом ступенів волі п-2 = 16-2 = 14 табличне значення критерія Стьюдента дорівнює = 2,145.

Для часового ряду доходів, виражених у млн грн, розрахункові значення tс і td перевищують табличне значення , тобто нульова гіпотеза не приймається, існує тренд як середнього, так і дисперсії ряду.

Для часового ряду доходів, виражених у відсотках до ВВП, розрахункові значення tс і td менші за табличне значення , тобто приймається гіпотеза про відсутність тренду в тенденції й дисперсії ряду. 

Розглянуті вище два методи перевірки стаціонарності часового ряду −  метод перевірки різниць середніх рівнів і Фостера−Стьюарта, дають різні результати щодо існування тренду дисперсії ряду доходів, виражених у % до ВВП. Якщо їхні висновки виявляються протилежними, перевагу віддають методу Фостера−Стьюарта.

Визначення типу нестаціонарності та ступеня інтеграції часового ряду. Стаціонарні ряди ще називаються динамічно стабільними або такими, що мають нульовий порядок інтеграції .

Порядком інтеграції є число, що показує, скільки разів часовий ряд потребує застосування оператора перших різниць, щоб стати стаціонарним рядом.

Позначимо через порядок інтеграції. Часовий ряд має одиничний корінь, або порядок інтеграції одиниця (), якщо є стаціонарним рядом, тобто ряд перших різниць має нульовий порядок інтеграції (). Часовий ряд має два одиничних корені, або порядок інтеграції 2, якщо його другі різниці є стаціонарним рядом: ; . У загальному випадку часовий ряд має порядок інтеграції : , якщо . Зазначимо, що якщо ряд стаціонарний, то будь-які його різниці залишаються стаціонарним рядом: тощо.

Тест Діккі – Фуллера призначений для того, щоб розрізняти часові ряди типу TS та DS. Відповідно нульовій гіпотезі досліджуваний ряд належить до типу DS. За альтернативною гіпотезою він може бути типу TS, але одночасно бути або нестаціонарним – мати детермінований тренд, або не мати тренду – бути стаціонарним. Виділяють простий тест Діккі – Фуллера − DF-тест та розширений тест Діккі – Фуллера − АDF-тест. Розглянемо їх по-порядку.

Простий DF-тест. Припустімо, що може бути описано моделлю:

,                                                                                     (1.3.9)

де випадкова величина є “білим шумом”. Зазначимо, що модель (1.3.9) увібрала в себе риси як DS, так і TS процесів. Якщо , то це випадкове блукання із дрейфом , тобто є нестаціонарним DS процесом. Якщо , тоді маємо справу зі стаціонарним марківським процесом. Зазначимо, що не набуває значень більших за 1, оскільки це передбачає вибуховий процес. Оскільки такі ряді мало імовірні в економічних дослідженнях, ми їх далі не розглядатимемо. Гіпотези щодо характеру ряда можна записати наступним чином:

: ряд є DS, якщо .

: ряд є TS, якщо .

В класичній лінійній регресії для перевірки такої гіпотези використовується одностороння -статистика. Для зведення процедури перевірки нульової гіпотези до більш звичної (коли коефіцієнт при дорівнює нулю) віднімемо з обох частин (1.3.9) . В результаті одержимо регресію:

,                             (1.3.10)

в якій перевіряємо наступну нульову гіпотезу проти альтернативної:

: ряд є DS, якщо ,

: ряд є TS, якщо .

Для звичайної регресії відношення порівнюється із критичним значенням -розподілу. Однак у випадку виконання гіпотези , ряд є випадковим блуканням, його дисперсія прагне до нескінченності при збільшенні часу, і розподіл -відношення не підпорядковується  -розподілу Стьюдента, а підпорядковується  розподілу Діккі – Фуллера (DF), який на відміну від позначається . Тест, який використовує для перевірки типу нестаціонарності цей розподіл, за умови , тобто коли процес належить типу DS, називається тестом Діккі – Фуллера.

Точна форма критерію значущості Діккі – Фуллера залежить від специфікації моделі, що підлягає тестуванню. Тому в загальному випадку розглядається  модель

,                                                   (1.3.11)

для якої можливі наступні три випадки перевірки нульової гіпотези і три критичні величини DF-розподілу, розраховані в таблицях МакКіннона [29]:

1. Модель без лінійного тренду та дрейфу (). Для цього розподілу критичне значення DF позначимо . Нульова гіпотеза означає, що = 1 і ряд − це випадкове блукання без дрейфу, тобто є нестаціонарним (інтегрованим) процесом: ~.
2. Модель тільки із додатною середньою (). Критичне значення DF − . Нульова гіпотеза означає, що = 1 і ряд − це випадкове блукання із дрейфом, тобто є нестаціонарним процесом: ~.
3. Модель з лінійним трендом та дрейфом (). Для цього розподілу критичне значення DF позначимо . Нульова гіпотеза означає, ряд − це випадкове блукання із двома типами тренду: стохастичним та детермінованим, тобто є нестаціонарним процесом ~.

Нульова гіпотеза буде відхилена, якщо -відношення має від’ємне значення, менше за критичне із таблиць МакКіннона. У цьому випадку часовий ряд − стаціонарний: ~ або має лінійний тренд () і після його вилучення стає стаціонарним.

Розширений АDF-тест. Його використання основане на припущенні, що замість білого шуму в моделі (1.3.12) випадкова складова  є стаціонарним авторегресійним процесом, наприклад, типу марківського, або у загальному випадку − типу ARMA(p,q). Тоді досліджується наступне рівняння:

.               (1.3.12)

У АDF-тесті перевіряється значущість лише одного коефіцієнту − . Наявність лагових прирощень та лагових значень випадкової змінної не змінює розподіл і можна користуватися тими ж таблицями Мак-Кіннона, що й для DF-тесту. Якщо в моделі (1.3.14) присутні і вільний член, і тренд, то нульову гіпотезу можна перевіряти, використовуючи статистику , якщо лише вільний член , то статистику , якщо немає ні того ні іншого, то потрібно використовувати статистику .

Для можливості застосування АDF-тесту важливо перевірити, що дисперсія випадкової величини є сталою, тобто випадкові збурення гомоскедастичні. Інакше, у випадку їх гетероскедастичності, тест вже неможливо застосувати. В комп’ютерному пакеті Ekonometric Views реалізований непараметричний тест Філліпса-Перрона (РР-тест) цієї перевірки.

Наступною важливою проблемою є те, що АDF-тест дуже чутливий до правильного вибору  значень та , які точно не відомі. Існує декілька способів її вирішення:

• застосувати правило узгодження кількості лагів, котрі потрібно включати в модель при застосуванні АDF-тесту, та довжиною часового ряду. В макроекономічних рядах, якщо маємо від 81 до 256 точок, то потрібно включати три лага. Якщо менше 81 точки, то два лага. Для фінансових рядів спрацьовує наближення , де квадратні дужки означають цілу частину числа.
• залишати таку кількість лагів, для яких оцінки МНК-коефіцієнтів при прирощеннях у (1.3.12) будуть статистично значущими за -розподілом Стьюдента.
• застосувати економетричний пакет Ekonometric Views, який містить алгоритм вибору кількості лагів.

Приклад 1.3.3. Перевірити за ADF-тестом, до якого типу (TS або DS) відноситься ряд індексу ділової активності для Великобританії (UK FTA All Share) [37].

1. Кількість лагів в моделі (1.3.17) була обрана трьом. Методом найменших квадратів оцінена наступна модель:

,

де -відношення для коефіцієнта при дорівнює –2,27. Критичне значення  на рівні значущості 5% дорівнює –3,49, тобто –2,27 > –3,49. Тому нульова гіпотеза не відхиляється і ряд належить до типу DS, тобто має одиничний корінь.

1. На другому кроці оцінюємо регресію виду:

,

тобто виключаємо з моделі  . -статистика коефіцієнту при лінійному тренду дорівнює 1.18. Порівнюємо її із таблицями нормального розподілу. Видно, що коефіцієнт не значущий, отже тренд не потрібно включати в модель. Тому переходимо до кроку 3.

1. Оцінюємо регресію виду:

,

Порівнюємо -відношення для коефіцієнта при із . Оскільки = -0,38, що набагато більше за критичне, то нульова гіпотеза не відхиляється. Але ще треба впевнитися у правильності включення в модель вільного члена.

1. Оцінюємо модель виду:

.

Тут − статистика, яка дорівнює 1,78, при порівнянні із критичною величиною стандартного нормального розподілу, виявляється значущою на 5-відсотковому рівні за одностороннім критерієм. Отже модель на кроці 3 специфікована правильно.

Загальний висновок полягає у тому, що ряд належить до типу DS і не містить лінійного тренду.

Встановлення типу нестаціонарності ряду не зводиться до однократного застосування тесту Діккі – Фуллера. Потрібне детальне дослідження правильності специфікації тестової моделі.

Якщо на першому етапі ADF-тесту нульова гіпотеза не може бути відхилена, то знов застосовується  ADF-тест, тільки вже для перевірки стаціонарності перших різниць ряду, а базове регресійне рівняння набуває виду других різниць:

.                                                              (1.3.13)

Модифікація критерію Дарбіна – Ватсона. Для часового ряду:

,                                                                      (1.3.14)

де u є випадковим блуканням

,  εt – білий шум,                                         (1.3.15)

оцінюють параметри й обчислюють статистику Дарбіна – Ватсона:

DW = .                                                                      (1.3.16)

Якщо запропонована модель (1.3.14) − (1.3.15) є коректною, з (1.3.16) очевидно, що чисельник у DW є сумою квадратів доданків білого шуму, а знаменник є сумою п доданків, кожен із яких (рекурентною підстановкою замість ut-1 у (1.3.10)) можна записати як нескінченну суму квадратів доданків білого шуму. Отже, значення статистики Дарбіна – Ватсона буде близьким до нуля, а критерій полягає у визначенні значущості його відмінності від нуля. Ця статистика називається коінтегративною регресійною статистикою Дарбіна – Ватсона (КРДВ), для якої розроблено таблиці критичних значень. Якщо для (1.3.14) статистика КРДВ не відмінна від нуля, доходять висновку, що є стаціонарним, а є нестаціонарним І(1)-процесом.

Дослідження автокореляційної функцій часового ряду (АКФ). На практиці порядок АКФ рекомендується обирати від п/4 до п/3. Значення коефіцієнта автокореляції, близьке до одиниці, вказує на значну додатну залежність між фактичним рядом даних і рядом, зрушеним на одиниць часу. У цьому разі пари спостережень будуть близькими один до одного. Якщо з’ясується, що більше спостереження утворює пару з меншим, то коефіцієнт автокореляції буде від’ємним і близьким до -1.

Корисною властивістю автокореляційної функцій є те, що для стаціонарних рядів існує деяке значення К таке, що для коефіцієнти автокореляції приймають майже нульові значення. Отже, якщо при збільшенні часового проміжку АКФ ряду за абсолютним значенням поступово згасає, ряд можна вважати стаціонарним. Якщо поведінка автокореляційні функції не така, то вона не може бути  автокореляційною функцією стаціонарного процесу. Для перевірки статистичної значущості коефіцієнтів автокореляції не існує простих критеріїв.

Перевірка за критерієм стандартної похибки коефіцієнта автокореляції. Якщо обсяг вибірки (п) великий, окремі (кожного порядку) коефіцієнти автокореляції випадкових даних мають вибірковий розподіл, який наближається до нормального з нульовим математичним сподіванням і середнім квадратичним відхиленням, що дорівнює

.                                                            (1.3.17), Якщо виходить за межі інтервалу , то часовий ряд має суттєву автокореляцію -го порядку. Зазначимо: якщо обчислено 20 значень АКФ, то на 5-відсотковому рівні значущості в середньому один із 20 буде значимим. Цей факт разом із відносно малим обсягом вибірки на практиці означає, що критерій на підставі окремих коефіцієнтів може бути ненадійним. Альтернативою є використання критерію Бокса − Пірса.

Q – к р и т е р і й  Б о к с а − П і р с а використовують для перевірки значущості всієї множини коефіцієнтів автокореляції як групи. Статистичний Q-критерій обчислюють за формулою:

,                                                       (1.3.18)

де − оцінка автокореляції порядку ;

    т − найбільший лаг, що розглядається.

Якщо всі автокореляції до порядку т дорівнюють нулю, то Q має приблизно -розподіл із т ступенями свободи. Велике значення Q порівняно з критичним зумовлює відхилення нульової гіпотези.

Існує кілька модифікацій цього критерію. Найпопулярнішим з них  є критерій Льюнга − Бокса:

.                                           (1.3.19)

Ці критерії можна також застосовувати до часткових автокореляцій.

 Приклад 1.3.4. За вибіркою у 28 спостережень про чисті податки на виробництво та імпорт розраховані коефіцієнти автокореляції. Результати розрахунків наведено в табл.1.3.4. Якщо коефіцієнт автокореляції першого порядку r1 перебуває в інтервалі:

-1,96·0,18  <  < 1,96·0,18 або остаточно -0,35 < < 0,35,

то можна вважати, що дані не вказують на наявність автокореляції першого порядку на рівні значущості 0,05. Розраховані коефіцієнти автокореляції від першого до четвертого порядків значно перевищують 0,35. Отже, можна зробити висновок про існування автокореляції для часового ряду чистих податків. Однак після четвертого порядку коефіцієнти автокореляції стають статистично незначущими.

Таблиця 1.3.4

Лаг	1	2	3	4	5	6	7	8	9	10	11	12
	0,66	0,46	0,49	0,55	0,26	0,12	0,10	0,26	0,07	0,06	0,05	0,07
	0,18	0,18	0,17	0,17	0,17	0,16	0,16	0,15	0,15	0,15	0,14	0,14

Статистичний критерій Q, наприклад із лагом у дванадцять часових інтервалів, дорівнює:

;  .

Отже, на 95% можна бути впевненими, що справжні коефіцієнти автокореляції для лагів у дванадцять періодів − не нульові (значущі). Це можна пояснити наявністю у ряду чистих податків сезонних коливань, порядок яких кратний чотирьом.

Ідентифікація детермінованого тренду та сезонності. Визначити, які невипадкові чинники, окрім випадкових, беруть участь у формуванні значень часового ряду, можна за допомогою автокореляційного аналізу. Сутність методу полягає в застосуванні апарату перших різниць і аналізу автокореляцій для ідентифікації часових рядів таких видів:

1) ряд не має тренду, якщо коефіцієнти автокореляції між рівнями ряду не залежать від часового лагу (статистично незначущі) і не мають певної закономірності зміни;

2) ряд має лінійний адитивний тренд у разі, коли автокореляційний аналіз вказує на лінійну залежність зміни коефіцієнтів автокореляції від часового лагу, а перехід до перших різниць виключає цю залежність;

3) ряд містить сезонну складову, якщо не існує лінійної залежності зміни коефіцієнтів автокореляції від часового лагу, але корелограма містить велику кількість значущих максимальних і мінімальних значень коефіцієнтів автокореляцій, що свідчить про значну залежність між спостереженнями, зрушеними на однаковий часовий інтервал;

4) ряд має лінійний тренд і сезонну складову, якщо його корелограма вказує на лінійну залежність зміни коефіцієнтів автокореляції від часового лагу і містить велику кількість значущих максимальних і мінімальних значень коефіцієнтів автокореляцій, а перехід до перших різниць виключає лінійний тренд, але статистична значущість певних коефіцієнтів автокореляцій залишається.

 Приклад 1.3.5. Проаналізуємо динаміку перевищення грошових доходів над витратами населення України за 2000-2001роки. На рис. 1.3.1 побудовано графік цього ряду, де середнє значення впродовж 24 місяців майже не змінюється й становить приблизно 324,4 млн.грн. Індивідуальні значення ряду коливаються навколо середнього, не виявляючи ані помітного зростання, ані сезонних змін. Отже, ряд має ознаки стаціонарного.

Рис.1.3.1. Стаціонарний ряд

 

Рис.1.3.2. Корелограма ряду без систематичної складової

 

Корелограму для цього ряду демонструє рис. 1.3.2. Точками позначено дві симетричні прямі, які визначають 95%-ві межі значущості коефіцієнта автокореляції (± дві стандартні похибки, тобто = 0,417, де п = 24. Точніше, п = 23 за k = 1 i п = 22 за k = 2 тощо). Оскільки жоден із коефіцієнтів автокореляції не лежить за цими межами, а в зміні значень коефіцієнтів відсутня певна закономірність, можна вважати, що в цьому разі часовий ряд показників не містить систематичної складової. 

Лінійний тренд. Лінійним трендом називають такий закон зміни середнього, за яким середнє зростає або спадає із часом за лінійною залежністю. Наприклад, попит на певний продукт може мати лінійний тренд що зростає, якщо продукт є для ринку новим товаром або якщо розширюється обсяг самого ринку за умов, що частка продукту залишається незмінною. Навпаки, якщо певний товар старіє, то тренд попиту на нього буде спадним. Криві зростання багатьох соціально-економічних показників можна звести до лінійного виду тренду. 

Адитивний тренд. В адитивних трендах фактичні значення відхиляються від середнього в більший чи менший бік приблизно на однакову величину. Наприклад, для лінійно-адитивного тренду середній приріст величини попиту за місяць може становити десять одиниць виміру.

Лінійно-адитивний тренд. Показник із таким видом тренду має середнє, яке зростає (або спадає) приблизно на однакову величину із кожним моментом часу. У разі лінійно-мультиплікативного тренду середнє є функцією часу, що зростає. Але у разі лінійно-адитивного тренду розкид відхилень фактичних значень навколо тренду приблизно постійний, тоді як у разі лінійно-мультиплікативного тренду цей розкид із часом збільшується.

 Приклад 1.3.6. На рис. 1.3.3 наведено лінійно-адитивний тренд щомісячної динаміки індексу цін споживчого ринку послуг за 2001 рік. Дослідження  корелограми для цих даних (рис.1.3.4) вказує на помітну залежність значень коефіцієнтів автокореляцій від величини лага. Коефіцієнти автокореляцій зменшуються зі збільшенням лага, максимальне значення відповідає лагу, який дорівнює одиниці (зрушення на один місяць), і становить 0,769; мінімальне значення коефіцієнта автокореляції відповідає зрушенню на 8 місяців і дорівнює -0,414. Така значна лінійна залежність унаочнює наявність лінійно-адитивного тренду.

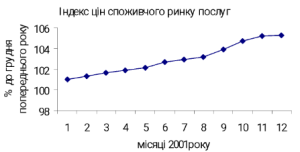
Рис. 1.3.3. Ряд із лінійно-адитивним трендом

Побудуємо для початкового ряду даних із лінійно-адитивним трендом ряд перших різниць і відповідну йому корелограму (рис. 1.3.5). Початковий ряд формально можна розглядати як ряд нульових різниць, тому корелограму, зображену на рис. 1.3.4, теж називають корелограмою нульових різниць.

Корелограма на рис. 1.3.5, після того як лінійно-адитивний тренд переходом до перших різниць був виключений, чітко показує, що перші різниці можна вважати випадково розкиданими, а рис. 1.3.2 і рис. 1.3.5 схожими за своєю хаотичністю. Отже, якщо автокореляційний аналіз вказує, що у значеннях коефіцієнтів автокореляцій нульових різниць (тобто початкового ряду) помітна строга лінійна залежність, а перехід до перших різниць усуває її, початковий ряд містить лінійно-адитивний тренд.

Рис. 1.3.4. Корелограма для випадку лінійно-адитивного тренду (нульові різниці)

Рис. 1.3.5. Корелограма для випадку лінійно-адитивного тренду (перші різниці) 

 

Сезонність. Ряд називають сезонним, якщо середнє змінюється циклічно відповідно до певного часового циклу. У більшості випадків на практиці цей часовий цикл залишається однаковим впродовж кількох років, причому середнє за кожен місяць порівняно із середнім за весь рік може і спадати, і підвищуватися. Сезонні коливання супроводжують динаміку попиту на такі товари, як одяг і взуття. До таких коливань схильні також потужні галузі промисловості (наприклад, коливання  попиту на автомобілі, що спадають із наближенням зими і зростають навесні).

 Приклад 1.3.7. На рис.1.3.6 зображено ряд із сезонними підвищеннями, що  припадають на літо й осінь, та спадами, що  припадають на зиму й весну. Лаг автокореляції має бути кратним 12, тобто січневе спостереження також слід порівнювати із січневим, але минулого року.

Рис.1.3.6. Сезонний ряд

Рис.1.3.7. Корелограма ряду із сезонним коливанням (нульові різниці)

Найбільші значення коефіцієнтів автокореляції, що спостерігаються для лагів у 12 і 24 місяці, дорівнюють відповідно 0,781 і 0,551, причому обидва ці коефіцієнти значущі (тобто перевищують 95%-ю межу довіри, яка в цьому разі дорівнює ±0,3). Ця обставина вказує на значну залежність між спостереженнями за один місяць, але для різних років. Навпаки, якщо лаг дорівнює 6 або 18 місяцям, тобто спостереження, яке відповідає підйому, порівнюється зі, спостереженням, яке відповідає спаду, коефіцієнт автокореляції має бути від’ємним. Це повністю підтверджується корелограмою, де мінімальні значення коефіцієнтів автокореляцій відповідають лагу в 6 і 18 місяців і дорівнюють -0,747 і -0,582 відповідно. Таким чином, показником суто сезонного ряду без лінійного тренду слугує корелограма із великим числом значущих максимальних і мінімальних значень коефіцієнтів  автокореляцій (що зображені на рис. 1.3.6). Оскільки на рис. 1.3.6 не виявляється лінійна залежність величини коефіцієнта автокореляції від величини лага, то початковий ряд не має лінійного тренду, тож перехід до перших різниць тут навряд чи доцільний.                                                                                   

 

Лінійний тренд із сезонно-адитивною складовою.

 Приклад 1.3.8. На рис. 1.3.8 зображено графік зміни дефлятора ВВП впродовж трьох років. Поряд із наявністю сезонної компоненти очевидною є присутність незначного, але сталого лінійного зростання. Корелограма для цих даних, тобто для нульових різниць, подана на рис.1.3.9.  Як видно із цього рисунка, існує значима додатна кореляція із лагом в 1 – 3 місяці, і від’ємна із лагом 22 – 24 місяці, що засвідчує наявність сезонних коливань ряду. На перший погляд автокореляція з лагом у 12 місяців незначуща, однак це наслідок того, що весь графік корелограми начебто розгорнутий по вертикалі під гострим кутом, тобто в ряду існують (і це очевидно) дані лінійного зростання. Чітко виражений графік корелограми ряду, який має сезонні коливання, розгорнутий відносно вертикалі на деякий кут, свідчить про наявність у початковому ряду лінійного тренду із сезонно-адитивною складовою.

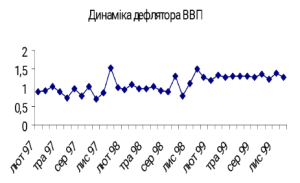
Рис. 1.3.8. Ряд із лінійним трендом та сезонно-адитивною складовою

 

Рис. 1.3.9. Корелограма ряду із лінійним трендом та сезонно-адитивною складовою (нульові різниці)

Якщо за такої ситуації тренд виключити переходом до перших різниць, то графік відповідної корелограми (рис. 1.3.10) буде вертикальний, і сезонність матиме вже не такий виразний характер. Однак значення коефіцієнтів автокореляції, що перебувають за 95%-ю межею довіри засвідчують наявність сезонних коливань.                                                         

 

Рис. 1.3.10. Корелограма ряду із лінійним трендом та сезонно-адитивною складовою  (перші різниці)

Мультиплікативні тренди, або тренди відношень. У мультиплікативних трендах збільшення або зменшення фактичного значення складає приблизно однаковий відсоток відносно середнього, яке визначається характером тренду. Наприклад, передбачається, що попит на певний товар із зростаючим лінійно-мультиплікативним трендом буде збільшуватися на 2% за місяць.

Комбінація адитивних і мультиплікативних трендів. Цей тип тренду є поєднанням двох трендів, розглянутих вище. Його вивчення досить складне, тому й застосовують його доволі нечасто.

Лінійно-мультиплікативний тренд. Значення показника за такого виду тренду перевершить (або буде меншим) попереднє значення приблизно на однаковий відсоток на всьому проміжку часу, що розглядається. На рис.1.3.11 зображено таку ситуацію. При цьому із часом збільшується не лише середнє, а й розкид індивідуальних значень навкруги середнього тренду.

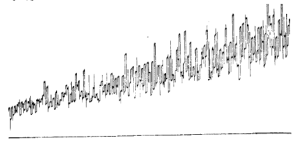
Рис. 1.3.11. Динаміка попиту із лінійно-мультиплікативним трендом

Комбінація лінійного і сезонно-адитивного тренду. Цей тип тренду може описувати також ситуацію суто сезонного тренду без лінійного елемента. Однак у загальному випадку для моделі цього типу характерна присутність сезонного тренду, який, своєю чергою, може лінійно зростати. Лінійний і сезонно-адитивний тренди зображені на рис.1.3.12. Як бачимо, з року в рік повторюються два викиди.

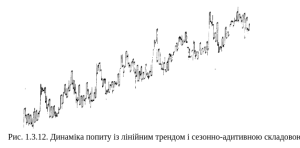
Рис. 1.3.12. Динаміка попиту із лінійним трендом і сезонно-адитивною складовою

 

Комбінація лінійного і сезонно-мультиплікативного тренду. Як і для комбінації лінійного і сезонно-адитивного трендів, аналітичне дослідження цього типу трендів

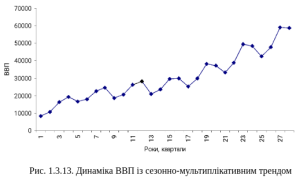
Рис. 1.3.13. Динаміка ВВП із сезонно-мультиплікативним трендом

передбачає і випадок суто сезонно-мультиплікативного тренду без лінійного зростання (рис.1.3.13), і випадок лінійного зростання.

 

Статистичні методи визначення наявності нелінійної динаміки й детермінованого хаосу. Належність часового ряду до випадкового процесу або детермінованого хаосу можна визначити за допомогою методу нормованого розмаху. 

Метод нормованого розмаху (R/S-аналіз) [29]. Застосування методу передбачає  такі кроки:

Крок 1. Визначають розмах:

,                                                                              (1.3.20)

де R – розмах відхилення Y;

– нагромадження відхилення за п періодів, , – рівень ряду в році и; – середнє за періодів;

– максимальне значення Y;

– мінімальне значення для Y;

Крок 2. Для різних часових періодів обчислюють – , де – відповідне нормованому розмаху середньоквадратичне відхилення.

Нормована величина розмаху функціонально пов’язана із таким чином:

,                                                                                              (1.3.21)

де – константа;   – показник Херста.

Крок 3. Оцінюється показник Херста як коефіцієнт регресії, рівняння якої виходить після логарифмування співвідношення (1.3.21):

.                                                                     (1.3.22)

Ця оцінка не має жодного припущення щодо розподілу випадкової величини.

За значенням показника Херста можна дійти таких висновків:

1) Якщо = 0,5 – економічний процес являє собою випадкове блукання, а розмах нагромаджених відхилень має збільшуватися пропорційно квадратному кореню від часу п.

2) . Цей діапазон відповідає ергодичним антиперсистентним рядам. Такий тип процесу часто називають «поверненням до середнього».

Антиперсистентний часовий ряд є більш мінливим, ніж ряд випадковий, оскільки складається із частих реверсів спад-підйом. Якщо процес демонструє зростання у попередньому періоді, то в наступному періоді найімовірніше почнеться спад. І навпаки, якщо відбувався спад, то імовірний близький підйом. Стійкість такої поведінки залежить від того, наскільки близьке до нуля. Чим ближче його значення до нуля, тим більше значення коефіцієнта від’ємної автокореляції рівнів часового ряду. Незважаючи на поширення концепції повернення до середнього в економічній й фінансовій літературі, досі було знайдено мало таких рядів.

3) При маємо персистентні, або тренд-стійкі ряди. Якщо ряд зростає (спадає) у попередній період, то він імовірно буде зберігати цю тенденцію певний час у майбутньому. Тренди очевидні. Трендо-стійкість поведінки, або сила персистентності, збільшується мірою наближення до одиниці, або 100% автокореляції. Чим ближче до 0,5, тим більше ряд зазнає впливу шуму і тим менш виражений його тренд.

Персистентний ряд – це узагальнений броунівський рух, або випадкові блукання із дрейфом. Сила зсуву залежить від того, наскільки перевищує 0,5. Такі ряди є нестабільними, вони властиві ринкам капіталу. Персистентний часовий ряд має довготривалу пам’ять, тому в ньому спостерігаються довготермінові кореляції між поточними подіями й подіями майбутніми.

Коли відрізняється від 0,50, це означає, що спостереження не є незалежними. Кожне спостереження несе пам’ять про всі минулі події. Це не короткотривала пам’ять, яку часто називають «марківською». Це інша пам’ять – довготривала, теоретично вона зберігається назавжди. Тобто нещодавні події справляють сильніший вплив, ніж події віддалені, але залишковий вплив останніх завжди відчутний.

8Приклад 1.3.9. У [29] розглянуто застосування R/S-аналізу до щомісячних даних із прибутків рейтингової компанії Стандард енд Пур (S&P 500) за 38-річний період від січня 1950 до липня 1988 року. Для цього виконуються такі кроки:

1) Вхідний часовий ряд (ціни), перетворюють на логарифмічний , де – логарифмічний прибуток в момент часу t; – ціна у момент часу t.

Для R/S-аналізу логарифмічні прибутки доцільніші, ніж широко використовувані відсоткові зміни цін, оскільки логарифмічні прибутки утворюють нагромаджений прибуток, який використовують в R/S-аналізі, тобто є нагромадженим відхиленням від середнього, чого не можна сказати про відсоткові зміни.

2) Рівняння (1.3.20) застосовують до різних часових періодів п. Ряд місячних даних, зафіксованих упродовж 40 років, містить 480 логарифмічних прибутків. Якщо починати із шестимісячних прирощень, можна розподілити ряд на 80 незалежних відрізків. Оскільки ці шестимісячні періоди не перекриваються, спостереження виявляються незалежними. (Вони можуть і не бути такими, якщо існують короткотермінові залежності марківського типу, які тривають понад шість місяців.) Отже, за  рівнянням (1.3.19) розраховують розмахи за кожним шестимісячним періодом і знаходять їхні нормовані значення. В результаті виходить 80 окремих R/S-спостережень. Шляхом осереднення цих спостережень одержуємо оцінку R/S для п = 6 місяцям.

Підрахунок продовжують для п = 7, 8, 9, . . . , 240. При цьому можна очікувати зменшення сталості оцінки R/S, оскільки зменшується кількість осереднюваних спостережень.

3) Сукупність розрахунків для всього діапазону п дає можливість визначити регресію log(R/S) на log(п) (1.3.21). На рис. 1.3.14 показана лінія регресії у подвійній логарифмічній шкалі. Нахил лінії регресії дає оцінку для =0,78. Однак оцінювати для повного діапазону п було б неправильним, бо ряд має обмежену пам’ять і починає поводитися як випадкове блукання. Процес із довготривалою пам’яттю спостерігається приблизно впродовж 48 місяців. Після цієї точки графік починає поводитися як випадкові блукання за = 0,50. Графіки на рис. 1.3.14 відповідають = 0,78 і = 0,50. За регресією для п > 48 місяців = 0,52 ± 0,02. Це підтверджує, що середня довжина циклу, або період для даних S&Р 500 дорівнює 18 місяцям.

Висока оцінка = 0,78 засвідчує, що фондовий ринок є очевидним нелінійним структурованим процесом і не поводиться як випадкове блукання. Для перевірки значущості одержаних результатів застосуємо до ряду щомісячних прибутків тест на змішування. На рис. 1.3.15 у логарифмічних координатах наведено криві змішаного й незмішаного рядів. Змішаний ряд явно відрізняється, показуючи = 0,51. Змішування руйнує структуру довготривалої пам’яті початкового ряду і перетворює його на ряд незалежний, що поводиться як випадкове блукання.

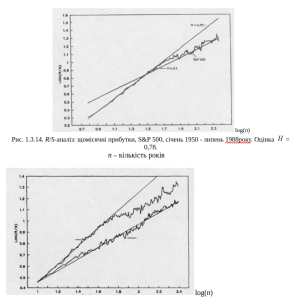
Рис. 1.3.15. Тест на змішування: S&P 500, щомісячні прибутки, січень 1950 – липень 1988 року. Незмішані дані: Н = 0,78, змішані дані: Н = 0,51.

R/S-аналіз показує, що часові ряди ринкових прибутків відповідають процесу випадкового блуканням із дрейфом. Разом із тим, такий процес циклічний і має тенденцію до середньої довжини циклу, що дорівнює 48 місяцям. Це саме середня величина, оскільки процес має складнішу структуру, ніж просто періодичну. 8

Перевірка нелінійності. Загального критерію нелінійності часового ряду не існує, оскільки вигляд статистик критеріїв залежить від конкретного типу нелінійності. Розглянемо один із критеріїв [14], що використовує автокореляційну функцію. Для лінійного інтегрованого процесу

,                                                                                    (1.3.23)

де і через позначено автокореляцію порядку . Тобто автокореляції є квадратами автокореляцій . Будь-яке порушення цієї умови відображає нелінійність динамічного процесу.